
| A. | $\frac{{x}^{2}}{2}$+$\frac{{y}^{2}}{3}$=1 | B. | 2x2+3y2=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1 | D. | 4x2+9y2=1 |
分析 根据题意,由伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{x′}{2}}\\{y=\frac{y′}{3}}\end{array}\right.$,将其代入方程x2+y2=1,进而化简即可得答案.
解答 解:根据题意,由伸缩变换$\left\{\begin{array}{l}{{x}^{′}=2x}\\{{y}^{′}=3y}\end{array}\right.$可得$\left\{\begin{array}{l}{x=\frac{x′}{2}}\\{y=\frac{y′}{3}}\end{array}\right.$,
将其代入方程x2+y2=1可得:($\frac{x′}{2}$)2+($\frac{y′}{3}$)2=1,
化简可得:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{9}$=1;
故选:C.
点评 本题考查直角坐标系中的伸缩变化,关键是掌握伸缩变化的公式.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知底面为正方形的四棱锥P-ABCD,如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4cm的全等的等腰直角三角形.
已知底面为正方形的四棱锥P-ABCD,如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4cm的全等的等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
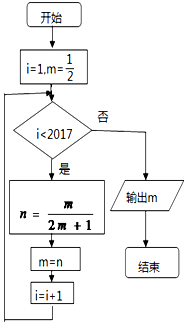
| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{4032}$ | D. | $\frac{1}{4034}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $S=\frac{100}{101},P=\frac{100}{101}$ | B. | $S=\frac{99}{100},P=\frac{99}{202}$ | ||
| C. | $S=\frac{100}{101},P=\frac{99}{202}$ | D. | $S=\frac{100}{101},P=\frac{99}{100}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.
如图,已知正方体ABC-A1B1C1D1中,AB=a,P为线段BC1上一点,Q为平面ABCD内一点,则D1P+PQ的最小值为(1+$\frac{\sqrt{2}}{2}$)a.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com