
| A. | 1 | B. | 2 | C. | 6 | D. | 4 |
分析 先画出约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$的可行域,再求出可行域中各角点的坐标,将各点坐标代入目标函数的解析式,分析后易得目标函数z=4x+2y的最大值.
解答  解:由约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$,得如图所示的三角形区域,
解:由约束条件$\left\{\begin{array}{l}x+y-1≥0\\ x-1≤0\\ 3x-y+1≥0\end{array}\right.$,得如图所示的三角形区域,
三个顶点坐标为A(1,4),B(1,0),C(0,1)
将三个代入z=4x+y-2,得z的值分别为6,2,-1.
直线z=4x+y-2过点A (1,4)时,z取得最大值为:6;
故选:C,
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:高中数学 来源: 题型:选择题
| A. | {3,4} | B. | {-2,3} | C. | {-2,4} | D. | {-1,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{32π}{3}$ | B. | 4π | C. | 6π | D. | $\frac{9π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
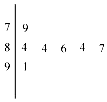 某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )
某学校举行的演讲比赛有七位评委,如图是评委们为某选手给出分数的茎叶图,根据规则去掉一个最高分和一个最低分.则此所剩数据的平均数和方差分别为( )| A. | 84,4.84 | B. | 84,1.6 | C. | 85,4 | D. | 85,1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com