【题目】已知不等式
的解集为
．
（1）求
的值；
（2）若不等式
的解集为
，不等式
的解集为
，且
，求实数
的取值范围.
【答案】（1）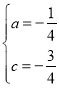
；（2）
.
【解析】
试题分析：（1）利用一元二次不等式的解集与相应的一元二次方程的实数根的关系即可求出；(2)“
”是“
”的充分不必要条件,将它们对应的不等式分别解出,可得集合
从而建立关于
的不等关系,解关于不等式即可得到实数的取值范围.
试题解析：（1）依题意得，1、3是方程
的两根，且
，．．．．．．．．．．．．．．．1分
所以，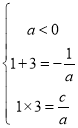
．．．．．．．．．．．．．．．．．．．．．．．．．．．．． 3分
解得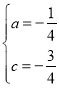；．．．．．．．．．．．．．．．．．．． 5分
（2）由（1）得
，所以，即为
，
解得，
，∴
，
又
，即为解得
，∴
，．．．．．．．．．．．．8分
∵
，∴，
∴
，即
，
∴
的取值范围是．．．．．．．．．．．．．．．10分
科目：高中数学 来源： 题型：
【题目】某地为制定初中七、八、九年级学生校服的生产计划，有关部门准备对180名初中男生的身高作调查．
（1）为了达到估计该地初中三个年级男生身高分布的目的，你认为采用怎样的调查方案比较合理？
（2）表中的数据是使用了某种调查方法获得的：七、八、九年级180名男生身高：
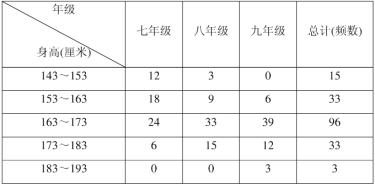
注：表中每组可含最低值，不含最高值．
根据表中的数据，请你给校服生产厂家指定一份生产计划思路．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，有一段河流，河的一侧是以O为圆心，半径为
米的扇形区域OCD，河的另一侧是一段笔直的河岸l，岸边有一烟囱AB（不计B离河岸的距离），且OB的连线恰好与河岸l垂直，设OB与圆弧
的交点为E．经测量，扇形区域和河岸处于同一水平面，在点C，点O和点E处测得烟囱AB的仰角分别为
，
和
．
（1）求烟囱AB的高度；
（2）如果要在CE间修一条直路，求CE的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系中，以坐标原点为极点，
轴为正半轴建立极坐标系，圆
的极坐标方程为
，直线
的参数方程为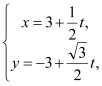
（t为参数）.
（1）求圆的直角坐标方程；
（2）求直线分圆所得的两弧程度之比.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如下图，已知四棱锥
中，底面
为菱形，
平面
，
，
，
分别是
，
的中点.
（I）证明：
平面
；
（II）取
，在线段
上是否存在点
，使得
与平面
所成最大角的正切值为
，若存在，请求出
点的位置；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某飞机失联，经卫星侦查，其最后出现在小岛
附近，现派出四艘搜救船
，为方便联络，船
始终在以小岛为圆心，100海里为半径的圆上，船构成正方形编队展开搜索，小岛在正方形编队外（如图）.设小岛到
的距离为
，
，
船到小岛的距离为
.
（1）请分别求关于
的函数关系式
，并分别写出定义域；
（2）当两艘船之间的距离是多少时搜救范围最大（即最大）？
查看答案和解析>>
科目：高中数学 来源： 题型：
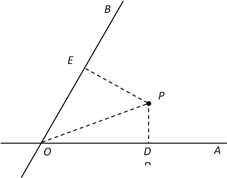
【题目】如图，
、
是两条公路（近似看成两条直线），
，在
内有一纪念塔
（大小忽略不计），已知到直线、的距离分别为
、
，=6千米，=12千米．现经过纪念塔修建一条直线型小路，与两条公路、分别交于点
、
．
（1）求纪念塔到两条公路交点
处的距离；
（2）若纪念塔为小路
的中点，求小路的长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】为增强市民的节能环保意识，郑州市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽取100名，其年龄频率分布直方图如图所示，其中年龄分组区是：
．
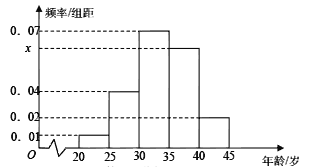
（Ⅰ）求图中
的值，并根据频率分布直方图估计这500名志愿者中年龄在
岁的人数；
（Ⅱ）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动，再从这10名志愿者中选取3名担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为
，求
的分布列及数学期望．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
