
【题目】已知抛物线![]() 的方程
的方程![]() 为抛物线
为抛物线![]() 上一点,
上一点,![]() 为抛物线的焦点.
为抛物线的焦点.
(I)求![]() ;
;
(II)设直线![]() 与抛物线
与抛物线![]() 有唯一公共点
有唯一公共点![]() ,且与直线
,且与直线![]() 相交于点
相交于点![]() ,试问,在坐标平面内是否存在点
,试问,在坐标平面内是否存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ?若存在,求出点
?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(I)![]() ;(II)存在,
;(II)存在,![]() .
.
【解析】
试题分析:(I)借助题设条件运用抛物线的定义求解;(II)借助题设运用直线与抛物线的位置关系及向量的数量积探求.
试题解析:
(I)由题可知![]() ,即
,即![]() ,由抛物线的定义可知
,由抛物线的定义可知![]() ............4分
............4分
(II)法1:由![]() 关于
关于![]() 轴对称可知,若存在点
轴对称可知,若存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则点
,则点![]() 必在
必在![]() 轴上,设
轴上,设![]() ,又设点
,又设点 ,由直线
,由直线![]() 与曲线
与曲线![]() 有唯一公共点
有唯一公共点![]() 知,直线
知,直线![]() 与
与![]() 相切由
相切由![]() 得
得![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得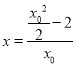 ,
,![]()
![]() 点坐标为
点坐标为![]() ,
,![]()
![]() ,
,![]()
![]() 点
点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,![]()
要使方程恒成立,必须有 ,解得
,解得![]() .
.
![]() 在坐标平面内存在点
在坐标平面内存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,其坐标为
,其坐标为![]() ..................12分
..................12分
法2:设点![]() ,由
,由![]() 与曲线
与曲线![]() 有唯一公共点
有唯一公共点![]() 知,直线
知,直线![]() 与
与![]() 相切,
相切,
由![]() 得
得![]() .
.![]() 直线
直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,
,![]()
![]() 点坐标为
点坐标为![]() ,
,
![]() 以
以![]() 为直径的圆的方程为:
为直径的圆的方程为: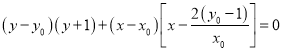 ①
①
分别令![]() 和
和![]() ,由点
,由点![]() 在曲线
在曲线![]() 上得
上得![]() ,
,
将![]() 的值分别代入①得:
的值分别代入①得:![]() ②
②
![]() ③
③
②③联立得![]() 或
或![]() .
.
![]() 在坐标平面内若存在点
在坐标平面内若存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则点
,则点![]() 必为
必为![]() 或
或![]() ,将
,将![]() 的坐标代入①式得,
的坐标代入①式得,
左边=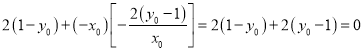 =右边,
=右边,
将![]() 的坐标代入①式得,左边=
的坐标代入①式得,左边=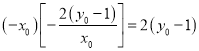 不恒等于0,
不恒等于0,
![]() 在坐标平面内若存在点
在坐标平面内若存在点![]() ,使得以
,使得以![]() 为直径的圆恒过点
为直径的圆恒过点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() .........12分
.........12分


科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处取得极值,求实数
处取得极值,求实数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,函数![]() (其中
(其中![]() 为函数
为函数![]() 的导数)的图像关于直线
的导数)的图像关于直线![]() 对称,求函数
对称,求函数![]() 单调区间;
单调区间;
(Ⅲ)在(Ⅱ)的条件下,若对任意的![]() ,都有
,都有![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列正确命题有__________.
①“![]() ”是“
”是“![]() ”的充分不必要条件
”的充分不必要条件
②如果命题“![]() ”为假命题,则
”为假命题,则![]() 中至多有一个为真命题
中至多有一个为真命题
③设![]() ,若
,若![]() ,则
,则![]() 的最小值为
的最小值为![]()
④函数![]() 在
在![]() 上存在
上存在![]() ,使
,使![]() ,则a的取值范围
,则a的取值范围![]() 或
或![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 相邻两对称轴间的距离为
相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图像先向左平移
的图像先向左平移![]() 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的对称中心;
的对称中心;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计,请你根据尚未完成的频率分布表和频率分布直方图,回答下面问题:
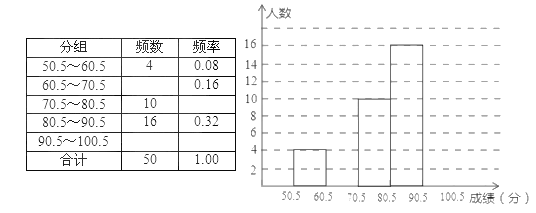
(1)结合图表信息,补全频率分布直方图;
(2)对于参加这次竞赛的900名学生,估计成绩不低于76分的约有多少人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某种微生物的生长规律,需要了解环境温度![]() (
(![]() )对该微生物的活性指标
)对该微生物的活性指标![]() 的影响,某实验小组设计了一组实验,并得到如表的实验数据:
的影响,某实验小组设计了一组实验,并得到如表的实验数据:
环境温度 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
活性指标 |
|
|
|
|
|
|
|
(Ⅰ)由表中数据判断![]() 关于
关于![]() 的关系较符合
的关系较符合![]() 还是
还是![]() ,并求
,并求![]() 关于
关于![]() 的回归方程(
的回归方程(![]() ,
,![]() 取整数);
取整数);
(Ⅱ)根据(Ⅰ)中的结果分析:若要求该种微生物的活性指标不能低于![]() ,则环境温度应不得高于多少
,则环境温度应不得高于多少![]() ?
?
附: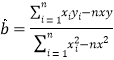 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《续古摘奇算法》(杨辉)一书中有关于三阶幻方的问题:将1,2,3,4,5,6,7,8,9分别填入![]() 的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
的方格中,使得每一行,每一列及对角线上的三个数的和都相等,我们规定:只要两个幻方的对应位置(如每行第一列的方格)中的数字不全相同,就称为不同的幻方,那么所有不同的三阶幻方的个数是( )
8 | 3 | 4 |
1 | 5 | 9 |
6 | 7 | 2 |
A. 9 B. 8 C. 6 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com