
(本题满分16分)已知函数 在
在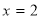 处的切线
处的切线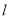 与直线
与直线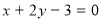 平行.
平行.
(1)求实数 的值;
的值;
(2)若关于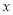 的方程
的方程 在
在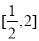 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)记函数 ,设
,设 是函数
是函数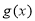 的两个极值点,若
的两个极值点,若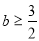 ,且
,且 恒成立,求实数
恒成立,求实数 的最大值.
的最大值.
(1)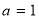 (2)
(2)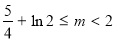 (3)
(3)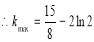
【解析】
试题分析:(1)由题知斜率为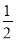 ,所以函数在
,所以函数在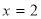 处的导数为
处的导数为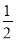 ,列出方程,解出
,列出方程,解出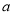
(2)构造函数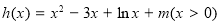 ,将有两个不相等的实根转化为函数有两上零点;然后求导,列表,根据图像列出不等式
,将有两个不相等的实根转化为函数有两上零点;然后求导,列表,根据图像列出不等式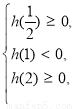 (3)由
(3)由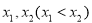 是函数
是函数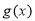 的两个极值点,求导得
的两个极值点,求导得
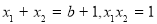 ,根据
,根据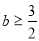 ,求出
,求出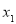 或
或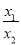 的范围;要求
的范围;要求 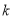 的最大值,即求
的最大值,即求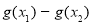 的最小值,根据
的最小值,根据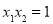 ,构造关于
,构造关于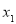 的函数,或直接构造关于
的函数,或直接构造关于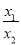 的函数, 求出最值。
的函数, 求出最值。
试题解析:【解析】
(1)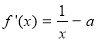 2分
2分
∵函数在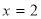 处的切线
处的切线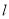 与直线
与直线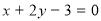 平行 ∴
平行 ∴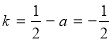 ,
,
解得: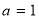 ; 4分
; 4分
(2)由(1)得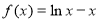 ,∴
,∴ ,即
,即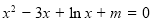
设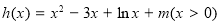 ,
,
则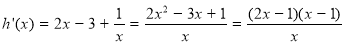
令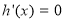 ,得
,得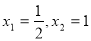 , 列表得:
, 列表得:
|
|
| 1 | (1,2) | 2 |
| 0 | - | 0 | + | |
| 极大值 |
| 极小值 |
|
|
∴当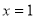 时,
时,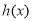 的极小值为
的极小值为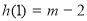 ,
,
又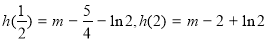 7分
7分
∵方程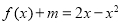 在
在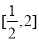 上恰有两个不相等的实数根,
上恰有两个不相等的实数根,
∴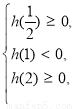 即
即 解得:
解得: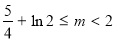 ;
;
(也可分离变量解) 10分
(3)解法(一)
∵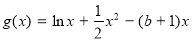 ,∴
,∴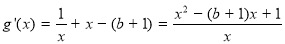
∴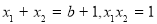 ,
,
∴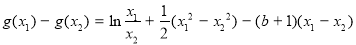
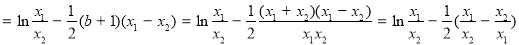
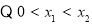 设
设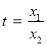 ,则
,则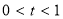 ,令
,令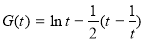 ,
,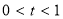
则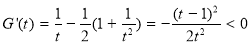 ,∴
,∴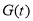 在
在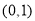 上单调递减; 12分
上单调递减; 12分
∵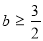 ,∴
,∴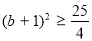
∵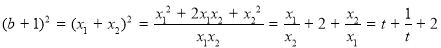
∴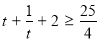 ∴
∴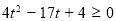 ∴
∴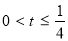 14分
14分
∴当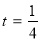 时,
时,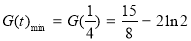 ∴
∴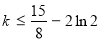
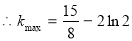 . 16分
. 16分
解法(二)
∵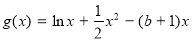 ,∴
,∴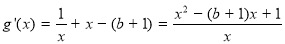
∴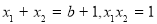 , ∴
, ∴ 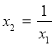 ∵
∵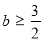 ∴
∴ 
解得: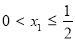 12分
12分
∴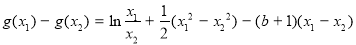
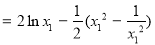
设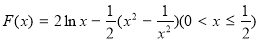 ,则
,则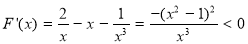
∴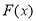 在
在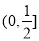 上单调递减; 14分
上单调递减; 14分
∴当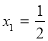 时,
时,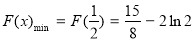 ∴
∴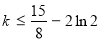
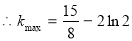 . 16分
. 16分
考点:导数的几何意义,导数与不等式


科目:高中数学 来源:2014-2015学年辽宁省高二上学期期末考试文科数学试卷(解析版) 题型:选择题
设变量x,y满足约束条件 ,则目标函数
,则目标函数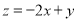 的最大值是( )
的最大值是( )
A.1 B.2 C.4 D.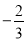
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高二文特班上学期第三次月考数学试卷(解析版) 题型:选择题
在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以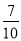 为概率的事件是
为概率的事件是
A.都不是一等品 B.恰有一件一等品
C.至少有一件一等品 D.至多一件一等品
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省高二文特班上学期第二次月考数学试卷(解析版) 题型:选择题
从装有除颜色外完全相同的2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是( ).
A.至少有1个白球,都是白球
B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球
D.至少有1个白球,都是红球
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省扬州市高二上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分14分)如图,斜三棱柱 中,侧面
中,侧面 是菱形,
是菱形, 与
与 交于点
交于点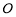 ,E是AB的中点.
,E是AB的中点.

求证:(1) 平面
平面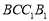 ;
;
(2)若 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江苏省扬州市高二上学期期末考试数学试卷(解析版) 题型:填空题
从集合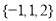 中随机选取一个数记为
中随机选取一个数记为 ,从集合
,从集合 中随机选取一个数记为
中随机选取一个数记为 ,则方程
,则方程 表示双曲线的概率为
表示双曲线的概率为
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省三明市高二上学期第二次月考理科数学试卷(解析版) 题型:填空题
一条长为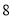 的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,则两个正方形的边长各是 ; ;
的铁丝截成两段,分别弯成两个正方形,要使两个正方形的面积和最小,则两个正方形的边长各是 ; ;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com