练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

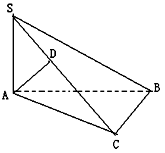
    已知在三棱锥S--ABC中，∠ACB=900，又SA⊥平面ABC，AD⊥SC于D，

    求证：AD⊥平面SBC

    见解析


    解析:

    证明：SA⊥面ABC， BC⊥面ABC，?? BC ⊥SA；

    又BC⊥AC，且AC、SA是面SAC内的两相交线，∴BC⊥面SAC；

    又AD??面SAC，∴ BC⊥AD，

    又已知SC⊥AD，且BC、SC是面SBC内两相交线，∴ AD⊥面SBC。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知正三棱锥S-ABC，斜高与底面ABC的夹角为α，在侧面SAB上有一点P，过P做底面ABC的高，垂足为Q，已知PQ=PS•sinα，求P点轨迹为（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：008

    判断正误:

    已知在三棱锥S-ABC中, △ABC是Rt△, ∠ACB＝90°, 且侧棱与底面ABC成角相等. 若点A在侧面SBC上的射影是H, 则H是△SBC的垂心.

    (　　)

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年广西桂林市、崇左市、防城港市高考第一次联合模拟理科数学试卷（解析版） 题型：填空题

    已知正三棱锥S－ABC的高为3，底面边长为6，过点A向它所对的侧面SBC作垂线，垂足为O，在AO上取一点P，使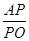=8，则过P且平行于底面的截面的面积为______.

     

    查看答案和解析>>

    科目：高中数学 来源：2012人教A版高中数学必修三3.3几何概型练习题（一）（解析版） 题型：解答题

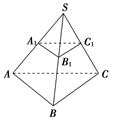
    已知正三棱锥S－ABC的底面边长为a，高为h，在正三棱锥内取一点M，试求点M到底面的距离小于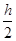的概率．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知正三棱锥S—ABC的高为3，底面边长为4，在正棱锥内任取一点P，使得的概率是（     ）

           A．                B．             C．                 D．

    查看答案和解析>>

    同步练习册答案