解:(1)法一:∵f(x)=x
2+ln(x-a)(a∈R),∴x>a,
∴
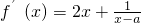
=
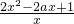
(x>a).
令g(x)=2x
2-2ax+1,△=4a
2-8=4(a
2-2).

当△>0时,得

或a

.
若a

,则f
′(x)>0在x>a时恒成立,此时函数f(x)无极值点;
若
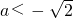
,设g(x)=2x
2-2ax+1=0的两根为x
1,x
2,且x
1<x
2.
∵
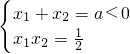
,∴a<x
1<x
2,若下表:
∴当
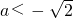
时,函数f(x)由两个极值点.
法二:
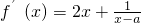
=
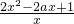
(x>a).
设g(x)=2x
2-2ax+1,f(x)由两个极值点?g(x)=0由两个大于a的不等实数根x
1,x
2(x
1<x
2).
∴

,解得
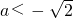
,∴当
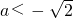
时,函数f(x)由两个极值点.
(2)当a≤-2时,由(1)知
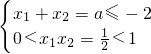
,∴a<x
1<-1<x
2<0.
∴f(x)在[-1,x
2]上为减函数,而在[x
2,0]上为增函数,
∴f(x)在[-1,0]上的最大值是f(-1)和f(0)中的最大的那一个.
∵f(-1)=1+ln(-1-a),f(0)=ln(-a).
设h(a)=f(-1)-f(0)=
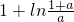
=
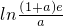
.
∵a≤-2,∴

,∴
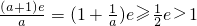
,故h(a)>0.
∴最大值为f(-1).
即g(a)=f(-1)=1+ln(-1-a)(a≤-2).
(3)由(2)可知:当a=-2时,f(x)=x
2+ln(x+2)有最大值f(-1)=1+ln(-1+2)=1.
取
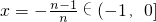
,n∈N
+.则
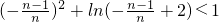
.
即
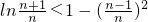
=
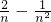
.
法一:由
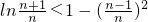
=
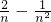
,
把n依次取n,n-1,…1得到n个不等式,再相加得:
ln(n+1)
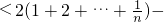
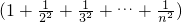
≤
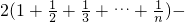
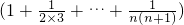
=

.
∴

.
即
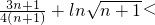
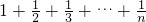
.
法二:用数学归纳法证明:
①当n=1时,易知成立.
假设n=k时,不等式成立,即
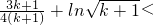
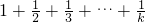
,(k∈N
+)成立.
当n=k+1时,
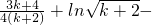
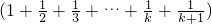
=
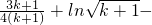
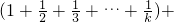
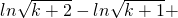
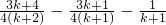
=
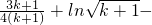
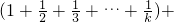
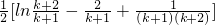
<
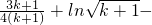
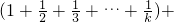

<0(由归纳假设及

.
所以当n=k+1时不等式也成立.
故得证.
分析:(1)f(x)有两个不同的极值点?f
′(x)=0在定义域内有不同的两个实数根.
(2)当a≤-2时,由(1)可知a<x
1<-1<x
2<0.及f(x)在[-1,x
2]与[x
2,0]上的单调性可得:f(x)在[-1,0]上的最大值是f(-1)和f(0)中的最大的那一个.
(3)利用(2)的结论可得:
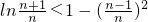
=
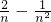
.把n依次取n,n-1,…1得到n个不等式,再相加即可得到.或利用上下归纳法也可证明.
点评:本题综合考查了利用导数解决含参数的函数的单调性和极值问题,熟练掌握导数、三个二次及分类讨论思想方法是解题的关键.

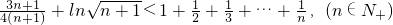 .
.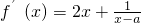 =
=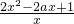 (x>a).
(x>a).
 或a
或a .
. ,则f′(x)>0在x>a时恒成立,此时函数f(x)无极值点;
,则f′(x)>0在x>a时恒成立,此时函数f(x)无极值点;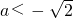 ,设g(x)=2x2-2ax+1=0的两根为x1,x2,且x1<x2.
,设g(x)=2x2-2ax+1=0的两根为x1,x2,且x1<x2.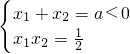 ,∴a<x1<x2,若下表:
,∴a<x1<x2,若下表: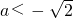 时,函数f(x)由两个极值点.
时,函数f(x)由两个极值点.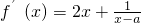 =
=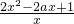 (x>a).
(x>a). ,解得
,解得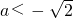 ,∴当
,∴当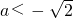 时,函数f(x)由两个极值点.
时,函数f(x)由两个极值点.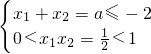 ,∴a<x1<-1<x2<0.
,∴a<x1<-1<x2<0.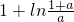 =
=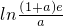 .
. ,∴
,∴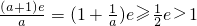 ,故h(a)>0.
,故h(a)>0.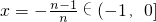 ,n∈N+.则
,n∈N+.则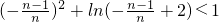 .
.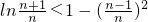 =
=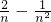 .
.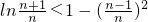 =
=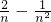 ,
,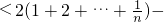
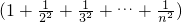
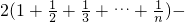
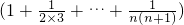 =
= .
. .
.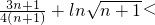
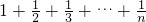 .
.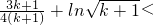
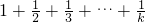 ,(k∈N+)成立.
,(k∈N+)成立.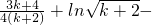
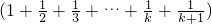
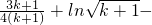
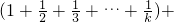
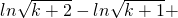
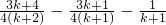
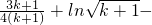
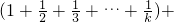
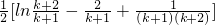
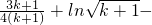
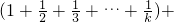

 .
.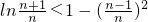 =
=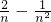 .把n依次取n,n-1,…1得到n个不等式,再相加即可得到.或利用上下归纳法也可证明.
.把n依次取n,n-1,…1得到n个不等式,再相加即可得到.或利用上下归纳法也可证明.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<