
【题目】随着移动互联网的发展,与餐饮美食相关的手机![]() 软件层出不穷,现从某市使用
软件层出不穷,现从某市使用![]() 和
和![]() 两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:
两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:

(1)使用![]() 订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个?
订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个?
(2)试估计该市使用![]() 款订餐软件的商家的“平均送达时间”的众数及中位数;
款订餐软件的商家的“平均送达时间”的众数及中位数;
(3)如果以“平均送达时间”的平均数作为决策依据,从![]() 和
和![]() 两款订餐软件中选择一款订餐,你会选择哪款?
两款订餐软件中选择一款订餐,你会选择哪款?
【答案】(1)40个(2)55;![]() (3)
(3)![]() 款
款
【解析】
(1)根据频率分布直方图计算出概率即可求出频数.
(2)利用频率分布直方图能求出使用![]() 款订餐软件的商家中“平均送达时间”的众数,中位数.
款订餐软件的商家中“平均送达时间”的众数,中位数.
(3)使用![]() 款订餐软件的商家中“平均送达时间”的平均数为35,小于
款订餐软件的商家中“平均送达时间”的平均数为35,小于![]() 款订餐软件的商家中“平均送达时间”的平均数40,以“平均送达时间”的平均数作为决策依据,从
款订餐软件的商家中“平均送达时间”的平均数40,以“平均送达时间”的平均数作为决策依据,从![]() 和
和![]() 两款订餐软件中选择
两款订餐软件中选择![]() 款订餐.
款订餐.
解:(1)使用![]() 款订餐软件的商家中“平均送达时间”不超过30分钟的商家共有
款订餐软件的商家中“平均送达时间”不超过30分钟的商家共有![]() 个.
个.
(2)依题意可得,使用![]() 款订餐软件的商家中“平均送达时间”的众数为55,
款订餐软件的商家中“平均送达时间”的众数为55,
由频率分布直方图可判断中位数位于![]()
设中位数为![]() ,则
,则![]() ,解得
,解得![]() .
.
(3)使用款![]() 订餐软件的商家中“平均送达时间”的平均数为
订餐软件的商家中“平均送达时间”的平均数为
![]()
使用![]() 款订餐软件的商家中“平均送达时间”的平均数为
款订餐软件的商家中“平均送达时间”的平均数为
![]()
所以选![]() 款订餐软件.
款订餐软件.


科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
, ![]() 是椭圆
是椭圆![]() 的左右焦点,
的左右焦点, ![]() 为椭圆
为椭圆![]() 的上顶点,点
的上顶点,点![]() 在椭圆
在椭圆![]() 上,直线
上,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
, ![]() 为坐标原点,且
为坐标原点,且![]() ,
, ![]() .
.
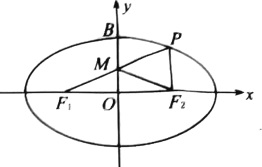
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作两条互相垂直的直线分别与椭圆
作两条互相垂直的直线分别与椭圆![]() 交于
交于![]() ,
, ![]() 两点(异于点
两点(异于点![]() ),证明:直线
),证明:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn,若Sm-1=-4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若数列{bn}满足![]() =log2bn(n∈N*),求数列{(an+6)·bn}的前n项和.
=log2bn(n∈N*),求数列{(an+6)·bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图①,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AD=CD=![]() AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC,如图②所示.
AB=2.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体DABC,如图②所示.

(1)证明:平面ABD⊥平面BCD;
(2)求二面角DABC的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2022年第24届冬奥会将在北京举行。为了推动我国冰雪运动的发展,京西某区兴建了“腾越”冰雪运动基地。通过对来“腾越”参加冰雪运动的100员运动员随机抽样调查,他们的身份分布如下: 注:将表中频率视为概率。
身份 | 小学生 | 初中生 | 高中生 | 大学生 | 职工 | 合计 |
人数 | 40 | 20 | 10 | 20 | 10 | 100 |
对10名高中生又进行了详细分类如下表:
年级 | 高一 | 高二 | 高三 | 合计 |
人数 | 4 | 4 | 2 | 10 |
(1)求来“腾越”参加冰雪运动的人员中高中生的概率;
(2)根据统计,春节当天来“腾越”参加冰雪运动的人员中,小学生是340人,估计高中生是多少人?
(3)在上表10名高中生中,从高二,高三6名学生中随机选出2人进行情况调查,至少有一名高三学生的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市![]() (如图)的东偏南
(如图)的东偏南![]() 方向300千米的海面
方向300千米的海面![]() 处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?
处,并以20千米/时的速度向西偏北45°方向移动,台风侵袭的范围为圆形区域,当前半径为60千米,并以10千米/时的速度不断增大,问几个小时后该城市开始受到台风的侵袭?受到台风的侵袭的时间有多少小时?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]() ,下列说法正确的是( )
,下列说法正确的是( )
A.若![]() 是函数
是函数![]() 的零点,则
的零点,则![]() 是
是![]() 的整数倍
的整数倍
B.函数![]() 的图象关于点
的图象关于点![]() 对称
对称
C.函数![]() 的图象与函数
的图象与函数![]() 的图象相同
的图象相同
D.函数![]() 的图象可由
的图象可由![]() 的图象先向上平移
的图象先向上平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度得到
个单位长度得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解某校学生喜欢吃零食是否与性别有关,随机对此校100人进行调查,得到如下的列表:已知在全部100人中随机抽取1人,抽到不喜欢吃零食的学生的概率为![]() .
.
喜欢吃零食 | 不喜欢吃零食辣 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 | 100 |
(Ⅰ)请将上面的列表补充完整;
(Ⅱ)是否有99.9%以上的把握认为喜欢吃零食与性别有关?说明理由.
下面的临界值表供参考:![]() ,其中
,其中![]()
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=|2x-1|-|x+1|.
(1)将f(x)的解析式写成分段函数的形式,并作出其图象;
(2)若a+b=1,对a,b∈(0,+∞),![]() +
+![]() ≥3f(x)恒成立,求x的取值范围.
≥3f(x)恒成立,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com