
【题目】已知f(x)=|2x-1|-|x+1|.
(1)将f(x)的解析式写成分段函数的形式,并作出其图象;
(2)若a+b=1,对a,b∈(0,+∞),![]() +
+![]() ≥3f(x)恒成立,求x的取值范围.
≥3f(x)恒成立,求x的取值范围.
【答案】(1)见解析(2)[-1,5]
【解析】试题分析:(1)讨论x的范围:x<﹣1,﹣1≤x≤![]() ,x>
,x>![]() ,去绝对值,可得f(x)的分段函数的解析式,由分段函数图象画法可得其图象;
,去绝对值,可得f(x)的分段函数的解析式,由分段函数图象画法可得其图象;
(2)运用乘1法和基本不等式,可得![]() +
+![]() 的最小值,由题意可得|2x﹣1|﹣|x+1|≤3,结合图象即可得到所求x的范围.
的最小值,由题意可得|2x﹣1|﹣|x+1|≤3,结合图象即可得到所求x的范围.
试题解析:
(1)由已知,得f(x)=
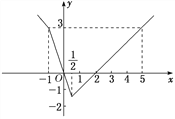
函数f(x)的图象如图所示.
(2)∵a,b∈(0,+∞),且a+b=1,
∴![]() +
+![]() =
=![]() (a+b)=5+
(a+b)=5+![]() ≥5+2
≥5+2![]() =9,当且仅当
=9,当且仅当![]() =
=![]() ,即a=
,即a=![]() ,b=
,b=![]() 时等号成立.
时等号成立.
∵![]() +
+![]() ≥3(|2x-1|-|x+1|)恒成立,
≥3(|2x-1|-|x+1|)恒成立,
∴|2x-1|-|x+1|≤3,
结合图象知-1≤x≤5,
∴x的取值范围是[-1,5].


科目:高中数学 来源: 题型:
【题目】随着移动互联网的发展,与餐饮美食相关的手机![]() 软件层出不穷,现从某市使用
软件层出不穷,现从某市使用![]() 和
和![]() 两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:
两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:

(1)使用![]() 订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个?
订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个?
(2)试估计该市使用![]() 款订餐软件的商家的“平均送达时间”的众数及中位数;
款订餐软件的商家的“平均送达时间”的众数及中位数;
(3)如果以“平均送达时间”的平均数作为决策依据,从![]() 和
和![]() 两款订餐软件中选择一款订餐,你会选择哪款?
两款订餐软件中选择一款订餐,你会选择哪款?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校微信公众号收到非常多的精彩留言,学校从众多留言者中抽取了100人参加“学校满意度调查”,其留言者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如下:
之间,根据统计结果,做出频率分布直方图如下:

(1)求这100位留言者年龄的平均数和中位数;
(2)学校从参加调查的年龄在![]() 和
和![]() 的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在
的留言者中,按照分层抽样的方法,抽出了6人参加“精彩留言”经验交流会,赠与年龄在![]() 的留言者每人一部价值1000元的手机,年龄在
的留言者每人一部价值1000元的手机,年龄在![]() 的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.
的留言者每人一套价值700元的书,现要从这6人中选出3人作为代表发言,求这3位发言者所得纪念品价值超过2300元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)如图(1)所示,椭圆的中心在原点,焦点F1、F2在x轴上,A、B是椭圆的顶点,P是椭圆上一点,且PF1⊥x轴,PF2∥AB,求此椭圆的离心率;
(2)如图(2)所示,双曲线的一个焦点为F,虚轴的一个端点为B,如果直线FB与该双曲线的一条渐近线垂直,求此双曲线的离心率.


查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:x2=2py (p>0) 的焦点,点A(m,3)在抛物线C上,且|AF|=5,若点P是抛物线C上的一个动点,设点P到直线![]() 的距离为
的距离为![]() ,设点P到直线
,设点P到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线C的方程;
(2) 求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某个部件由三个元件按如图所示的方式连接而成,元件1或元件2正常工作,且元件3正常工作,则部件正常工作.设三个电子元件的使用寿命(单位:时)均服从正态分布N(1000,502),且各个元件能否正常工作相互独立,那么该部件的使用寿命超过1000小时的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABC-A1B1C1的所有棱长都为2,D为CC1中点.
(1)求证:AB1⊥平面A1BD;
(2)求锐二面角A-A1D-B的余弦值;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com