
分析 (I)由$\overrightarrow{m}$∥$\overrightarrow{n}$,可得asinB-$\sqrt{3}$bcosA=0,再利用正弦定理即可得出..
(II)S=$\frac{1}{2}bcsin\frac{π}{3}$=$\frac{3\sqrt{3}}{2}$,化为:bc=6.由余弦定理可得:$(\sqrt{7})^{2}$=b2+c2-2bccos$\frac{π}{3}$,化简可得b+c.
解答 解:(I)∵$\overrightarrow{m}$∥$\overrightarrow{n}$,∴asinB-$\sqrt{3}$bcosA=0,
由正弦定理可得:sinAsinB-$\sqrt{3}$sinBcosA=0,sinB≠0,可得tanA=$\sqrt{3}$,
A∈(0,π),∴A=$\frac{π}{3}$.
(II)S=$\frac{1}{2}bcsin\frac{π}{3}$=$\frac{3\sqrt{3}}{2}$,化为:bc=6.
由余弦定理可得:$(\sqrt{7})^{2}$=b2+c2-2bccos$\frac{π}{3}$,解得b2+c2-bc=7,∴(b+c)2-3bc=7,可得b+c=5.
∴三角形的周长=5+$\sqrt{7}$.
点评 本题考查了正弦定理余弦定理、向量共线定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 转速x(转/秒) | 2 | 4 | 5 | 6 | 8 |
| 每小时生产有缺点的零件数y(件) | 30 | 40 | 60 | 50 | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
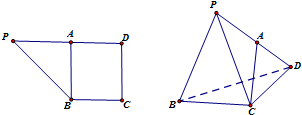 如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.
如图,矩形ABCD和直角三角形ABP有共同的边AB,且PA=AD=3,DC=4,沿BD把平面DBP折起,使AC=$\sqrt{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com