|
|
|
已知a∈R,函数f(x)=x·|x-a|.
(1)当a=2时,写出函数f(x)的单调递增区间(不必证明);
(2)当a>2时,求函数y=f(x)在区间[1,2]上的最小值;
(3)设a≠0,函数f(x)在区间(m,n)上既有最小值又有最大值,请分别求出m、n的取值范围(用a表示).
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
设函数f(x)= 为奇函数,则a=________. 为奇函数,则a=________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
设a∈R,函数f(x)=x·|x-a|+2x.
(1)若a=2,求函数f(x)在区间[0,3]上的最大值;
(2)若a>2,写出函数f(x)的单调区间(不必证明);
(3)若存在a∈[-2,4],使得关于x的方程f(x)=t·f(a)有三个不相等的实数解,求实数t的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
若a<b,则下列不等式成立的是
|
| [ ] |
A. |
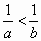
|
B. |

|
C. |

|
D. |
不确定
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
已知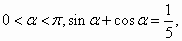 求sinα-cosα的值. 求sinα-cosα的值.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
已知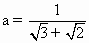 , ,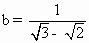 ,则a、b的等差中项是 ,则a、b的等差中项是
|
| [ ] |
A. |

|
B. |
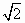
|
C. |
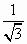
|
D. |
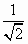
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
设等差数列{an}的前n项和为Sn,且a5+a13=34,S3=9.数列{bn}的前n项和为Tn,满足Tn=1-bn.
(1)求数列{an}的通项公式;
(2)写出一个正整数m,使得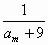 是数列{bn}的项; 是数列{bn}的项;
(3)设数列{cn}的通项公式为 ,问:是否存在正整数t和k(k≥3),使得c1,c2,ck成等差数列?若存在,请求出所有符合条件的有序整数对(t,k);若不存在,请说明理由. ,问:是否存在正整数t和k(k≥3),使得c1,c2,ck成等差数列?若存在,请求出所有符合条件的有序整数对(t,k);若不存在,请说明理由.
|
|
|
查看答案和解析>>
科目:高中数学
来源:2015届山东省高三上学期11月检测考试文科数学试卷(解析版)
题型:解答题
(本小题满分12分)设向量 .
.
(1)若 ,求
,求 的值;
的值;
(2)设函数 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学
来源:2015届山东省德州市高三10月月考文科数学试卷(解析版)
题型:解答题
已知函数 ,
,
(1)求函数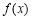 的对称轴所在直线的方程;
的对称轴所在直线的方程;
(2)求函数 单调递增区间.
单调递增区间.
查看答案和解析>>

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案