已知直线ax-2by=2(a>0,b>0)过圆x2+y2-4x+2y+1=0的圆心,ab的最大值为 .
【答案】
分析:把圆的方程化为标准形式,求出圆心,再根据直线过圆心可得a+b=1,再利用基本不等式求得ab的最大值.
解答:解:圆x
2+y
2-4x+2y+1=0 即 (x-2)
2+(y+1)
2=4,表示以C(2,-1)为圆心,半径等于2的圆.
由于直线ax-2by=2(a>0,b>0)过圆心,故有 2a+2b=2,即 a+b=1.
再由基本不等式可得a+b=1≥2
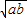
,∴ab≤

,当且仅当a=b=

时,取等号,
故ab的最大值为1,
故答案为 1.
点评:本题主要考查圆的标准方程,基本不等式的应用,属于中档题.
