练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，四边形为平行四边形，且，点E，F为平面外两点，且，．

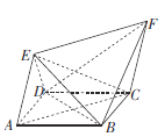
    （1）证明：；

    （2）若，求异面直线与所成角的余弦值．

    【答案】（1）详见解析；（2）．

    【解析】

    （1）证明平面，再利用线面垂直的定义，即可得到线线垂直；

    （2）证明直线，，两两互相垂直，分别以，，为x，y，z轴建立空间直角坐标系，求得，，再利用向量的夹角公式计算，即可得到答案；

    解：（1）设与相交于点G，连接，

    由题意可得四边形为菱形，所以，，

    在和中，，，，

    所以，所以，所以，因为，所以平面，

    因为平面，所以．

    （2）如图，在平面内，过G作的垂线，交于点，由（1）可知，平面平面，

    所以平面，故直线，，两两互相垂直，

    分别以，，为x，y，z轴建立空间直角坐标系，

    因为，

    则，，，，

    所以，，

    异面直线与所成角的余弦值为．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，已知椭圆过点，离心率为，分别是椭圆的左、右顶点，过右焦点且斜率为的直线与椭圆相交于两点．

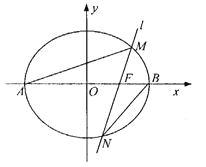
    （1）求椭圆的标准方程；

    （2）记、的面积分别为、，若，求的值；

    （3）记直线、的斜率分别为、，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率e满足，以坐标原点为圆心，椭圆C的长轴长为半径的圆与直线相切.

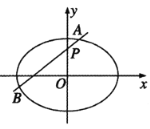
    （1）求椭圆C的方程；

    （2）过点P(0，1)的动直线(直线的斜率存在)与椭圆C相交于A，B两点，问在y轴上是否存在与点P不同的定点Q，使得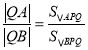恒成立？若存在，求出定点Q的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数的图象如图所示，给出四个函数：①，②，③，④，又给出四个函数的图象，则正确的匹配方案是（ ）．

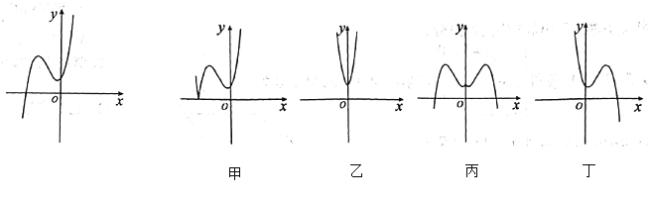
    A.①－甲，②－乙，③－丙，④－丁B.②－甲，①－乙，③－丙，④－丙

    C.①－甲，③－乙，④－丙，②－丁D.①－甲，④－乙，③－丙，②－丁

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】图1，在中，，，E为中点.以为折痕将折起，使点C到达点D的位置，且为直二面角，F是线段上靠近A的三等分点，连结，，，如图2.

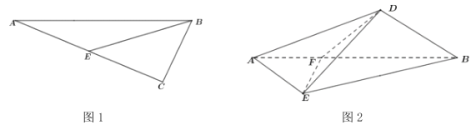
    （1）证明：；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学高三年级在返校复学后，为了做好疫情防护工作，一位防疫督察员要将2盒完全相同的口罩和3盒完全相同的普通医用口罩全部分配给3个不同的班，每个班至少分得一盒，则不同的分法种数是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在多面体中，平面平面，，，，，．

    （1）求平面与平面所成二面角的正弦值；

    （2）若是棱的中点，求证：对于棱上任意一点，与都不平行．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=|lnx|，g（x）=，则方程|f（x）+g（x）|=1实根的个数为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C的参数方程为（为参数），直线，以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系.

    （1）求直线l和曲线C的极坐标方程；

    （2）若直线与直线l相交于点A，与曲线C相交于不同的两点M，N.求的最小值.

    查看答案和解析>>

    同步练习册答案