
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
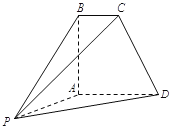
(1)求平面![]() 与平面
与平面![]() 所成二面角的正弦值;
所成二面角的正弦值;
(2)若![]() 是棱
是棱![]() 的中点,求证:对于棱
的中点,求证:对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)解法一,由面面垂直的条件证明![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() ,这样以点
,这样以点![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,分别求平面
轴,建立空间直角坐标系,分别求平面![]() 和平面
和平面![]() 的法向量
的法向量![]() ,根据公式
,根据公式![]() 计算;解法二:在平面
计算;解法二:在平面![]() 内,过点
内,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ;在平面
;在平面![]() 内,过
内,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() .连接
.连接![]() ,根据垂直关系,说明
,根据垂直关系,说明![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角;
所成二面角的平面角;
(2)解法一:假设存在点![]() 满足
满足![]() ,设
,设![]() ,
,![]() ,并利用向量相等表示点
,并利用向量相等表示点![]() 的坐标,若满足
的坐标,若满足![]() ,则
,则![]() ,利用向量相等,列方程组求解判断是否有解;解法二:假设棱
,利用向量相等,列方程组求解判断是否有解;解法二:假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,显然
,显然![]() 与点
与点![]() 不同,所以
不同,所以![]() 四点共面,利用四点共面推出矛盾;解法三:假设棱
四点共面,利用四点共面推出矛盾;解法三:假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,在△
,在△![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,由条件可知
的中点,由条件可知![]() ,
,![]() 都平行于
都平行于![]() ,推出矛盾.
,推出矛盾.
解法一:(1)因为![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
作![]() 交
交![]() 于
于![]() ,则
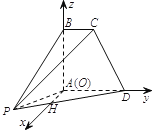
,则![]() 三条直线两两垂直.以
三条直线两两垂直.以![]() 为坐标原点
为坐标原点![]() ,分别以
,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,如图所示.
轴,建立空间直角坐标系,如图所示.
因为![]() ,
,![]() ,
,![]() .
.
所以![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,因为
,因为![]() ,
,
所以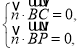 所以
所以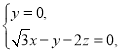 令
令![]() ,所以
,所以![]() ,
,
由![]() 轴
轴![]() 平面
平面![]() 知
知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
所以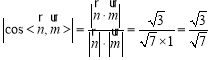 ,
,
所以![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.
(2)因为![]() 是棱
是棱![]() 的中点,由(1)可得
的中点,由(1)可得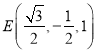 .
.
假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,
,
设![]() ,
,![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以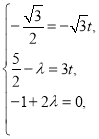 这个方程组无解,
这个方程组无解,
所以假设不成立,所以对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
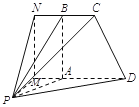
解法二:(1)如图,在平面![]() 内,过点
内,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ;在平面
;在平面![]() 内,过
内,过![]() 作
作![]() 的垂线,交
的垂线,交![]() 的延长线于点
的延长线于点![]() .连接
.连接![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
设平面![]() 平面
平面![]() ,则
,则![]() ,故
,故![]() 平面
平面![]() .
.
所以![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的平面角.
所成二面角的平面角.
因为![]() ,
,![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() .
.
又![]() ,所以在
,所以在![]() 中,
中,![]() .
.
所以![]() ,
,
所以![]() 与平面
与平面![]() 所成二面角的正弦值为
所成二面角的正弦值为![]() .
.
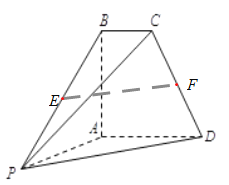
(2)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() ,显然
,显然![]() 与点
与点![]() 不同
不同
所以![]() 四点共面,记该平面为
四点共面,记该平面为![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 就是点
就是点![]() 确定的平面,
确定的平面,
这与![]() 为四棱锥相矛盾,所以假设不成立,
为四棱锥相矛盾,所以假设不成立,
所以对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.
解法三:(1)同解法一.
(2)假设棱![]() 上存在点
上存在点![]() ,使得
,使得![]() .
.
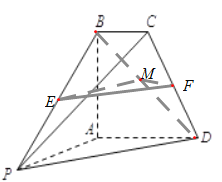
连接![]() ,取
,取![]() 的中点
的中点![]() ,
,
在△![]() 中,因为
中,因为![]() 分别为
分别为![]() 的中点,
的中点,
所以![]() .
.
因为过直线外一点有且只有一条直线和已知直线平行,所以![]() 与
与![]() 重合.
重合.
又点![]() 在线段
在线段![]() 上,所以
上,所以![]() ,又
,又![]() ,
,
所以![]() 是
是![]() 与
与![]() 的交点
的交点![]() ,即
,即![]() 就是
就是![]() ,
,
而![]() 与
与![]() 相交,所以与
相交,所以与![]() 相矛盾,所以假设不成立,
相矛盾,所以假设不成立,
所以对于棱![]() 上任意一点
上任意一点![]() ,
,![]() 与
与![]() 都不平行.
都不平行.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
【题目】给定下列四个命题,其中真命题是( )
A.垂直于同一直线的两条直线相互平行
B.若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行
C.垂直于同一平面的两个平面相互平行
D.若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台仪器每启动一次都随机地出现一个![]() 位的二进制数
位的二进制数![]() ,其中
,其中![]() 的各位数字中,
的各位数字中,![]() 出现
出现![]() 的概率为
的概率为![]() ,出现
,出现![]() 的概率为
的概率为![]() .若启动一次出现的数字为
.若启动一次出现的数字为![]() ,则称这次试验成功.若成功一次得
,则称这次试验成功.若成功一次得![]() 分,失败一次得
分,失败一次得![]() 分,则
分,则![]() 次这样的重复试验的总得分
次这样的重复试验的总得分![]() 的数学期望和方差分别为( )
的数学期望和方差分别为( )
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两种树苗中各抽测了10株树苗的高度,其茎叶图数据如图.根据茎叶图,下列描述正确的是( )
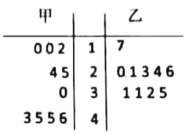
A.甲种树苗的中位数大于乙种树苗的中位数,且甲种树苗比乙种树苗长得整齐
B.甲种树苗的中位数大于乙种树苗的中位数,但乙种树苗比甲种树苗长得整齐
C.乙种树苗的中位数大于甲种树苗的中位数,且乙种树苗比甲种树苗长得整齐
D.乙种树苗的中位数大于甲种树苗的中位数,但甲种树苗比乙种树苗长得整齐
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为贯彻落实党中央全面建设小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康,2019年6月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入,作出散点如下:
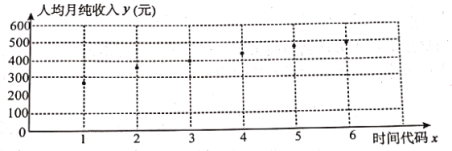
根据盯关性分析,发现其家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系(记2019年1月、2月……分别为
之间具有较强的线性相关关系(记2019年1月、2月……分别为![]() ,
,![]() ,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入只有2019年12月的预估值的
,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入只有2019年12月的预估值的![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求该家庭2020年3月份的人均月纯收入;
(3)如果以该家庭3月份人均月纯收入为基数,以后每月增长率为![]() ,问该家庭2020年底能否实现小康生活?
,问该家庭2020年底能否实现小康生活?
参考数据:![]() ,
,![]() ,
,![]()
参考公式: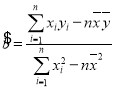 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com