
【题目】在直角坐标系xOy中,曲线C的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() ,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.
(1)求直线l和曲线C的极坐标方程;
(2)若直线![]() 与直线l相交于点A,与曲线C相交于不同的两点M,N.求
与直线l相交于点A,与曲线C相交于不同的两点M,N.求![]() 的最小值.
的最小值.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】为贯彻落实党中央全面建设小康社会的战略部署,某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作.经过多年的精心帮扶,截至2018年底,按照农村家庭人均年纯收入8000元的小康标准,该地区仅剩部分家庭尚未实现小康,2019年6月,为估计该地能否在2020年全面实现小康,统计了该地当时最贫困的一个家庭2019年1至6月的人均月纯收入,作出散点如下:
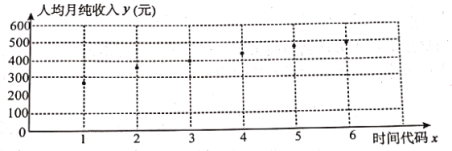
根据盯关性分析,发现其家庭人均月纯收入![]() 与时间代码
与时间代码![]() 之间具有较强的线性相关关系(记2019年1月、2月……分别为
之间具有较强的线性相关关系(记2019年1月、2月……分别为![]() ,
,![]() ,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入只有2019年12月的预估值的
,…,依此类推),由此估计该家庭2020年能实现小康生活.但2020年1月突如其来的新冠肺炎疫情影响了奔小康的进展,该家庭2020年第一季度每月的人均月纯收入只有2019年12月的预估值的![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)求该家庭2020年3月份的人均月纯收入;
(3)如果以该家庭3月份人均月纯收入为基数,以后每月增长率为![]() ,问该家庭2020年底能否实现小康生活?
,问该家庭2020年底能否实现小康生活?
参考数据:![]() ,
,![]() ,
,![]()
参考公式: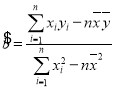 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知多面体![]() 是正方体,
是正方体,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点,点
的中点,点![]() 是棱
是棱![]() 上的动点,过点
上的动点,过点![]() ,
,![]() ,
,![]() 的平面与棱
的平面与棱![]() 交于点
交于点![]() ,则以下说法不正确的是( )
,则以下说法不正确的是( )
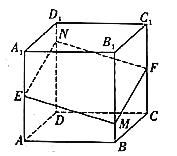
A.四边形![]() 是平行四边形
是平行四边形
B.四边形![]() 是菱形
是菱形
C.当点![]() 从点
从点![]() 往点
往点![]() 运动时,四边形
运动时,四边形![]() 的面积先增大后减小
的面积先增大后减小
D.当点![]() 从点
从点![]() 往点
往点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积一直增大
的体积一直增大
查看答案和解析>>
科目:高中数学 来源: 题型:
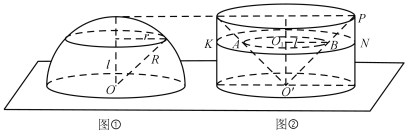
【题目】祖暅原理指出:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等,例如在计算球的体积时,构造一个底面半径和高都与球的半径相等的圆柱,与半球(如图①)放置在同一平面上,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥后得到一新几何体(如图②),用任何一个平行于底面的平面去截它们时,可证得所截得的两个截面面积相等,由此可证明新几何体与半球体积相等.现将椭圆![]() 所围成的平面图形绕y轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
所围成的平面图形绕y轴旋转一周后得一橄榄状的几何体,类比上述方法,运用祖暅原理可求得其体积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,且
,且![]() .过椭圆的右焦点
.过椭圆的右焦点![]() 作长轴的垂线与椭圆,在第一象限交于点
作长轴的垂线与椭圆,在第一象限交于点![]() ,且满足
,且满足![]() .
.
(1)求椭圆的标准方程;
(2)若矩形![]() 的四条边均与椭圆相切,求该矩形面积的取值范围.
的四条边均与椭圆相切,求该矩形面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新型冠状病毒引发的疫情牵动着亿万人的心,八方驰援战疫情,众志成城克时难,社会各界支援湖北共抗新型冠状病毒肺炎,重庆某医院派出3名医生,2名护士支援湖北,现从这5人中任选2人定点支援湖北某医院,则恰有1名医生和1名护士被选中的概率为( )
A.0.7B.0.4C.0.6D.0.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】CPI是居民消费价格指数的简称,是一个反映居民家庭一般所购买的消费品和服务项目价格水平变动情况的宏观经济指标.同比一般情况下是今年第n月与去年第n月比;环比,表示连续2个统计周期(比如连续两月)内的量的变化比.如图是根据国家统计局发布的2019年4月—2020年4月我国CPI涨跌幅数据绘制的折线图,根据该折线图,则下列说法正确的是( )
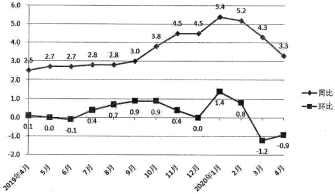
A.2020年1月CPI同比涨幅最大
B.2019年4月与同年12月相比较,4月CPI环比更大
C.2019年7月至12月,CPI一直增长
D.2020年1月至4月CPI只跌不涨
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
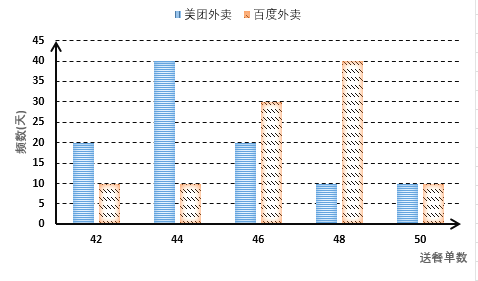
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com