
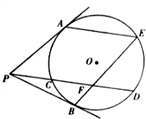
 如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.
如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.分析 (Ⅰ)连接AB,利用P、B、F、A四点共圆,PA与圆O切于点A,得出两组角相等,即可证明:AE∥CD;
(Ⅱ)四边形PBFA的外接圆就是四边形PBOA的外接圆,OP是该外接圆的直径,由切割线定理可得PA,即可求四边形PBFA的外接圆的半径.
解答  ( I)证明:连接AB.
( I)证明:连接AB.
∵P、B、F、A四点共圆,∴∠PAB=∠PFB. …(2分)
又PA与圆O切于点A,∴∠PAB=∠AEB,…(4分)
∴∠PFB=∠AEB∴AE∥CD.…(5分)
( II)解:因为PA、PB是圆O的切线,所以P、B、O、A四点共圆,
由△PAB外接圆的唯一性可得P、B、F、A、O共圆,
四边形PBFA的外接圆就是四边形PBOA的外接圆,∴OP是该外接圆的直径.…(7分)
由切割线定理可得PA2=PC•PD=3×9=27 …(9分)
∴$OP=\sqrt{P{A^2}+O{A^2}}=\sqrt{27+25}=2\sqrt{13}$.
∴四边形PBFA的外接圆的半径为$\sqrt{13}$.…(10分)
点评 本题考查四点共圆,考查圆的切线的性质,考查切割线定理的运用,考查学生分析解决问题的能力,属于中档题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| 体积(升/件) | 重量(公斤/件) | 利润(元/件) | |
| 甲 | 20 | 10 | 8 |
| 乙 | 10 | 20 | 10 |
| A. | 65元 | B. | 62元 | C. | 60元 | D. | 56元 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
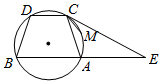 如图,已知圆上的$\widehat{AC}$=$\widehat{BD}$,过C点的圆的切线与BA的延长线交于E点,设M是$\widehat{AC}$的中点,
如图,已知圆上的$\widehat{AC}$=$\widehat{BD}$,过C点的圆的切线与BA的延长线交于E点,设M是$\widehat{AC}$的中点,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=$\frac{kπ}{2}$-$\frac{π}{6}$(k∈Z) | B. | x=$\frac{kπ}{2}$+$\frac{π}{6}$(k∈Z) | C. | x=$\frac{kπ}{2}$-$\frac{π}{12}$(k∈Z) | D. | x=$\frac{kπ}{2}$+$\frac{π}{12}$(k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com