
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 分别构造新函数,结合函数的单调性分别判断即可.
解答 解:①当xf′(x)-f′(x)>0即(x-1)f′(x)>0时,
f(x)在(-∞,1)递减,在(1,+∞)递增,
故f(x)的最小值是f(1),函数f(x)存在最小值,
故①正确;
②令g(x)=xf(x),g′(x)=xf′(x)+f(x)
当xf′(x)+f(x)>0时,
函数g(x)=xf(x)在R递增,
故函数f(x)在R上不一定单调递增,
比如f(x)=1是常函数,
故②错误;
③令g(x)=$\frac{f(x)}{{e}^{x}}$,则g′(x)=$\frac{f′(x)-f(x)}{{e}^{x}}$,
当f′(x)-f(x)>0时,
g′(x)>0,g(x)在R递增,
∴g(n)<g(n+1),
即$\frac{f(n)}{{e}^{n}}$<$\frac{f(n+1)}{{e}^{n+1}}$,
∴ef(n)<f(n+1),n∈N*,
故③正确;
④令g(x)=f(x)-3x,则g′(x)=f′(x)-3
∵f′(x)<3,∴g′(x)<0,g(x)递减,
而f(1)=4,∴g(1)=4-3=1,
不等式f(lnx)>3lnx+1,
即g(lnx)>g(1),即lnx<1,
故不等式的解集为(0,e),
故④正确,
故选:C.
点评 本题考查了函数的单调性问题,考查导数的应用,构造出新函数是解题的关键,本题是一道中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
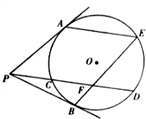 如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.
如图所示,过点P分别做圆O的切线PA、PB和割线PCD,弦BE交CD于F,满足P、B、F、A四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
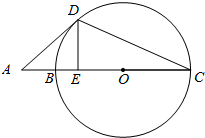 过点A和圆心O的直线交⊙O于B,C两点(AB<AC),AD与⊙O切于点D,DE⊥AC于E,AD=3$\sqrt{5}$,AB=3,则BE的长度为( )
过点A和圆心O的直线交⊙O于B,C两点(AB<AC),AD与⊙O切于点D,DE⊥AC于E,AD=3$\sqrt{5}$,AB=3,则BE的长度为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $\frac{1}{2}$ | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.8 | B. | 0.6 | C. | 0.4 | D. | 0.3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com