
分析 (Ⅰ)求出f′(x),解不等式f′(x)>0,f′(x)<0可函数的单调区间,利用函数的单调性和导数之间的关系,即可求函数f(x)的最小值;
(Ⅱ)要使f(x)≥0对任意的x∈R恒成立,则只需求出f(x)的最小值即可得到结论.
(III)利用ln(1+x)<x,x∈(0,1),可得ln[1+$\frac{2^n}{{({2^{n-1}}+1)({2^n}+1)}}}$]<$\frac{2^n}{{({2^{n-1}}+1)({2^n}+1)}}}$=2$(\frac{1}{{2}^{n-1}+1}-\frac{1}{{2}^{n}+1})$,即可证明.
解答 (Ⅰ)解:∵f′(x)=ex-a,
当a>0时,若x∈(lna,+∞),f′(x)>0,得函数f(x)在(lna,+∞)上是增函数;
若x∈(-∞,lna),f′(x)<0,得函数f(x)在(-∞,lna)上是减函数.
则当a>0时,函数f (x) 的单调递增区间是(lna,+∞),单调递减区间是(-∞,lna).
即f(x)在x=lna处取得极小值且为最小值,
最小值为f(lna)=elna-alna-1=a-alna-1.
(Ⅱ)解:若f(x)≥0对任意的x∈R恒成立,
等价为f(x)min≥0,
由(Ⅰ)知,f(x)min=a-alna-1,
设g(a)=a-alna-1,
则g′(a)=1-lna-1=-lna,
由g′(a)=0得a=1,
由g′(x)>0得,0<x<1,此时函数单调递增,
由g′(x)<0得,x>1,此时函数单调递减,
∴g(a)在a=1处取得最大值,即g(1)=0,
因此g(a)≥0的解为a=1.
(III)证明:∵ln(1+x)<x,x∈(0,1).
∴ln[1+$\frac{2^n}{{({2^{n-1}}+1)({2^n}+1)}}}$]<$\frac{2^n}{{({2^{n-1}}+1)({2^n}+1)}}}$=2$(\frac{1}{{2}^{n-1}+1}-\frac{1}{{2}^{n}+1})$,
∴ln(1+$\frac{2}{2×3}$)+ln(1+$\frac{4}{3×5}$)+ln(1+$\frac{8}{5×9}$)+…+ln[1+$\frac{2^n}{{({2^{n-1}}+1)({2^n}+1)}}}$]
<2$[(\frac{1}{2}-\frac{1}{2+1})$+$(\frac{1}{2+1}-\frac{1}{{2}^{2}+1})$+…+$(\frac{1}{{2}^{n-1}+1}-\frac{1}{{2}^{n}+1})]$=2$(\frac{1}{2}-\frac{1}{{2}^{n}+1})$<1.
点评 本题考查了利用导数研究函数的单调性极值点、证明不等式、“裂项求和”方法、放缩法,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2) | B. | (-∞,0) | C. | (2,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OB=OC=2.E、F分别是AB、AC的中点,过EF作平面与侧棱OA,OB,OC或其延长线分别相交于A1、B1、C1.
如图,正三棱锥O-ABC的三条侧棱OA,OB,OC两两垂直,且OA=OB=OC=2.E、F分别是AB、AC的中点,过EF作平面与侧棱OA,OB,OC或其延长线分别相交于A1、B1、C1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.
如表是一个由n2个正数组成的数表,用aij表示第i行第j个数(i,j∈N),已知数表中第一列各数从上到下依次构成等差数列,每一行各数从左到右依次构成等比数列,且公比都相等.已知a11=1,a31+a61=9,a35=48.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北正定中学高二上月考一数学(文)试卷(解析版) 题型:解答题
执行如图所示的程序框图.
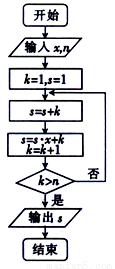
(1)若输入的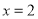 ,
,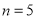 ,求输出的
,求输出的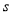 的值;
的值;
(2)若输入的 ,输出的
,输出的 ,求输入的
,求输入的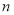 (
(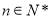 )的值.
)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com