
分析 (I) 求出f′(x)=$\frac{(lnx+1)(x-1)-xlnx}{(x-1)^{2}}$=$\frac{x-lnx-1}{(x-1)^{2}}$,(x>0,且x≠1),设μ(x)=x-lnx-1,则${μ}^{'}(x)=1-\frac{1}{x}=\frac{x-1}{x}$,由此利用导数性质能求出f(x)单调区间.
(Ⅱ)由已知$φ(x)=ln({x+1})+\frac{1}{2}a{x^2}-ax>0$对x>0恒成立,$φ'(x)=\frac{1}{x+1}+ax-a=\frac{{a{x^2}+1-a}}{x+1}$,由此利用分类讨论思想能求出a的取值范围.
解答 解:(I)∵函数f(x)=$\frac{xlnx}{x-1}$,
∴f′(x)=$\frac{(lnx+1)(x-1)-xlnx}{(x-1)^{2}}$=$\frac{x-lnx-1}{(x-1)^{2}}$,(x>0,且x≠1),
设μ(x)=x-lnx-1,则${μ}^{'}(x)=1-\frac{1}{x}=\frac{x-1}{x}$,
x∈(0,1)时,μ′(x)<0;x∈(1,+∞)时,μ′(x)<0,
∴u(x)在(0,1)上单减,在(1,+∞)上单增,
∴u(x)≥u(1)=0,
∴f(x)的增区间为(0,1),(1,+∞),无单调减区间.(5分)
(Ⅱ)∵?x>0,f(x+1)>g(x)成立,
即$φ(x)=ln({x+1})+\frac{1}{2}a{x^2}-ax>0$对x>0恒成立,
$φ'(x)=\frac{1}{x+1}+ax-a=\frac{{a{x^2}+1-a}}{x+1}$,(6分)
①当0≤a≤1时,φ'(x)≥0,则φ(x)在(0,+∞)上单调递增,
∴φ(x)>φ(0)=0,满足题意.(8分)
②当a>1时,令φ'(x)<0,则$0<x<\sqrt{\frac{a-1}{a}}$,
∴φ(x)在$(0,\sqrt{\frac{a-1}{a}})$上单调递减,∴x∈$(0,\sqrt{\frac{a-1}{a}})$时,∴φ(x)<φ(0)=0,不满足题意.(10分)
③当a<0时,令φ'(x)>0,则$0<x<\sqrt{\frac{a-1}{a}}$,
∴φ(x)在$(0,\sqrt{\frac{a-1}{a}})$上单调递增,在$(\sqrt{\frac{a-1}{a}},+∞)$上单调递减.(11分)
取${x_0}=2(1-\frac{1}{a})∈(\sqrt{\frac{a-1}{a}},+∞)$时,
当x>0时,ln(x+1)<x,
$φ({x_0})=ln({{x_0}+1})+\frac{1}{2}a{x_0}^2-a{x_0}<{x_0}+\frac{1}{2}a{x_0}^2-a{x_0}$,
∴$φ({x_0})<\frac{1}{2}a{x_0}^2+(1-a){x_0}=\frac{1}{2}a{x_0}[{x_0}-\frac{2(a-1)}{a}]=0$,不满足题意.
综上所述:a的取值范围[0,1].(14分)
说明:∵$φ({x_0})=ln({{x_0}+1})+\frac{1}{2}a{x_0}^2-a{x_0}<{x_0}+\frac{1}{2}a{x_0}^2-a{x_0}$
在x→+∞时,${x_0}+\frac{1}{2}a{x_0}^2-a{x_0}→-∞$,不合题意,学生这样做也可给满分.
点评 本题考查函数的单调区间的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质、分类讨论思想和构造法的合理运用.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
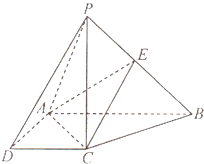 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AB∥DC,∠ADC=90°,PC=AB=2AD=2DC=2,点E为PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,AB∥DC,∠ADC=90°,PC=AB=2AD=2DC=2,点E为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
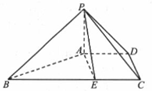 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com