
| A. | (1,$\sqrt{2}$) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | (1,$\frac{2\sqrt{3}}{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
分析 确定双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线方程,求得A,B的坐标,利用90°<∠AFB<120°,可得1<kFB<$\sqrt{3}$,
运用两点的斜率公式和a,b,c的关系,由此可求双曲线的离心率的取值范围.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的两条渐近线的两条渐近线方程为y=±$\frac{b}{a}$x,
x=$\frac{{a}^{2}}{c}$时,y=±$\frac{ab}{c}$,
∴A($\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),B($\frac{{a}^{2}}{c}$,-$\frac{ab}{c}$),
∵90°<∠AFB<120°,F(c,0),
由对称性可得tan45°<kFB<tan60°,
即有1<$\frac{\frac{ab}{c}}{c-\frac{{a}^{2}}{c}}$<$\sqrt{3}$,
即为1<$\frac{a}{b}$<$\sqrt{3}$,
而e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$∈($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$).
故选:D.
点评 本题考查双曲线的方程和性质,主要是渐近线方程和离心率的求法,考查学生的计算能力,正确寻找几何量之间的关系是关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{12}$,0)对称 | B. | 关于直线x=$\frac{5π}{12}$对称 | ||
| C. | 关于点($\frac{5π}{12}$,0)对称 | D. | 关于直线x=$\frac{π}{12}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
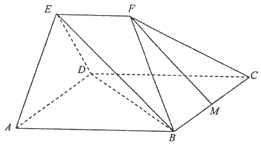 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
某一考点有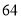 个试室,试室编号为
个试室,试室编号为 ,现根据试室号,采用系统抽样的方法,抽取
,现根据试室号,采用系统抽样的方法,抽取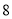 个试室进行监控抽查,已抽看了
个试室进行监控抽查,已抽看了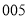 试室号,则下列可能被抽到的试室号是
试室号,则下列可能被抽到的试室号是
A.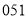 B.
B.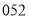 C.
C.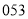 D.
D.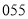
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com