
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\sqrt{2}$) | B. | ($\frac{2\sqrt{3}}{3}$,+∞) | C. | (1,$\frac{2\sqrt{3}}{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西省高一上学期第一次月考数学试卷(解析版) 题型:选择题
非空数集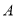 如果满足:①
如果满足:① ;②若对
;②若对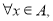 有
有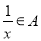 ,则称
,则称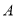 是“互倒集”.给出以下数集:
是“互倒集”.给出以下数集:
①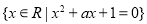 ;
;
②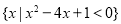 ;
;
③ .其中“互倒集”的个数是( )
.其中“互倒集”的个数是( )
A.0 B.3 C.2 D.1
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:填空题
已知高一年级有学生450人, 高二年级有学生750人, 高三年级有学生600人.用分层抽样从该校的这三个年级中抽取一个样本, 且每个学生被抽到的概率为0.02, 则应从高二年级抽取的学生人数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com