
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
分析 根据题意,由抛物线的方程可得抛物线焦点坐标,即可得双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的焦点坐标,即可得c的值,再双曲线的离心率公式可得e=$\frac{c}{a}$=$\sqrt{3}$,解可得a的值,由双曲线的性质可得b的值,将a、b的值代入双曲线方程即可得答案.
解答 解:根据题意,抛物线y2=12x的焦点在x轴正半轴上,其坐标为(3,0),
则双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1中,一个焦点的坐标为(3,0),即c=3,
又由双曲线的离心率e=$\sqrt{3}$,则有e=$\frac{c}{a}$=$\sqrt{3}$,解可得a=$\sqrt{3}$,
则b2=c2-a2=6,
则双曲线的标准方程为:$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1;
故选:D.
点评 本题考查双曲线、抛物线的几何性质,关键是掌握双曲线中a、b、c的关系.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
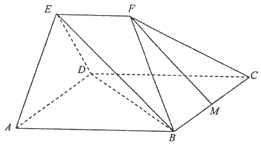 已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.
已知:平行四边形ABCD中,∠DAB=45°,AB=$\sqrt{2}$AD=2$\sqrt{2}$,平面AED⊥平面ABCD,△AED为等边三角形,EF∥AB,EF=$\sqrt{2}$,M为线段BC的中点.查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:解答题
设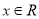 ,函数
,函数 ,
,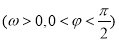 .已知
.已知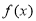 的最小正周期为
的最小正周期为 ,且
,且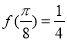 .
.
(1)求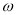 和
和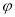 的值;
的值;
(2)求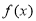 的单调递增区间;
的单调递增区间;
(3)求函数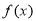 在区间
在区间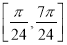 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
在等差数列{an}中,已知a5=15,则a2+a4+a6+a8的值为( )
A.30 B.45 C.60 D.120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com