
分析 (Ⅰ)利用三角恒等变换化简函数f(x)为正弦型函数,根据正弦函数的有界性求出f(x)的值域;
(Ⅱ)由题设条件与三角函数的图象和性质可知f(x)的周期为π,求出ω的值,再根据正弦函数的单调性求出f(x)的单调递减区间.
解答 解:(Ⅰ)函数f(x)=2sin(ωx+$\frac{π}{6}$)-4cos2$\frac{ωx}{2}$+3
=2($\frac{\sqrt{3}}{2}$sinωx+$\frac{1}{2}$cosωx)-2cosωx+1
=2($\frac{\sqrt{3}}{2}$sinωx-$\frac{1}{2}$cosωx)+1
=2sin(ωx-$\frac{π}{6}$)+1,
由-1≤sin(ωx-$\frac{π}{6}$)≤1,
得-1≤2sin(ωx-$\frac{π}{6}$)+1≤3,
∴函数f(x)的值域为[-1,3];
(Ⅱ)由题设条件与三角函数的图象和性质可知,
函数f(x)的周期为π,
即$\frac{2π}{ω}$=π,解得ω=2;
∴f(x)=2sin(2x-$\frac{π}{6}$)+1;
令2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$(k∈Z),
解得kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$(k∈Z);
∴函数f(x)的单调递减区间是[kπ+$\frac{π}{3}$,kπ+$\frac{5π}{6}$](k∈Z).
点评 本题考查了三角恒等变换以及正弦型函数的图象和性质的应用问题,是中档题.


科目:高中数学 来源: 题型:解答题
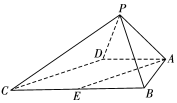 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,1} | B. | {1,3} | C. | {-1,1,3} | D. | {-3,-1,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{27}$-$\frac{{y}^{2}}{18}$=1 | B. | $\frac{{y}^{2}}{18}$-$\frac{{x}^{2}}{27}$=1 | C. | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | D. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{6}$=1 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西省高一上学期第一次月考数学试卷(解析版) 题型:选择题
设A,B是全集I={1,2,3,4}的子集,A={l,2},则满足A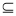 B的B的个数是( )
B的B的个数是( )
A.5 B.4 C.3 D.2
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河北省高二文上第一次月考数学试卷(解析版) 题型:选择题
三棱锥P-A BC的四个顶点都在球D的表面上,PA⊥平面ABC,AB⊥BC,PA =3,AB=BC=2,则球O的表面积为( )
A.13π B.17π C.52π D.68π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com