
分析 (1)将点代入椭圆方程,由椭圆的离心率公式求得a2=4b2,即可求得a和b的值,求得椭圆方程;
(2)分类讨论,当直线l斜率不为0时,设直线l的方程,代入椭圆方程,由韦达定理及向量数量积的坐标运算,即可求得m的值,求得直线方程.
解答 解:(1)由已知将$M({\sqrt{3},\frac{1}{2}})$代入椭圆方程:$\frac{3}{a^2}+\frac{1}{{4{b^2}}}=1$,①
由题意的离心率e=$\frac{c}{a}$=$\frac{{\sqrt{{a^2}-{b^2}}}}{a}=\frac{{\sqrt{3}}}{2}$,a2=4b2,②
由①②,解得:a=2,b=1,
∴椭圆Γ的方程为$\frac{x^2}{4}+{y^2}=1$;
(2)由已知N的坐标为$({\sqrt{3},0})$,
当直线l斜率为0时,直线l为x轴,易知$\overrightarrow{NB}+3\overrightarrow{NA}=0$不成立.
当直线l斜率不为0时,设直线l的方程为$x=my+\sqrt{3}$,
代入$\frac{x^2}{4}+{y^2}=1$,整理得,$({4+{m^2}}){y^2}+2\sqrt{3}my-1=0$,
设A(x1,y1),B(x2,y2),
则${y_1}+{y_2}=\frac{{-2\sqrt{3}m}}{{4+{m^2}}}$,①${y_1}{y_2}=\frac{-1}{{4+{m^2}}}$,②
由$\overrightarrow{NB}+3\overrightarrow{NA}=0$,得y2=-3y1,③
由①②③解得$m=±\frac{{\sqrt{2}}}{2}$.
所以直线l的方程为$x=±\frac{{\sqrt{2}}}{2}y+\sqrt{3}$,即$y=±\sqrt{2}({x-\sqrt{3}})$,
直线l的方程$y=±\sqrt{2}({x-\sqrt{3}})$.
点评 本题考查椭圆的标准方程,直线与椭圆的位置关系,考查韦达定理,向量数量积的坐标运算,考查计算能力,属于中档题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | -14 | C. | 14 | D. | 30 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $1+\sqrt{5}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\sqrt{5}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| t | [0,15) | [15,30) | [30,45) | [45,60) | [60,75) | [75,90) |
| 男同学人数 | 7 | 11 | 15 | 12 | 2 | 1 |
| 女同学人数 | 8 | 9 | 17 | 13 | 3 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年河南省新乡市高二上学期入学考数学卷(解析版) 题型:解答题
设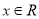 ,函数
,函数 ,
,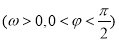 .已知
.已知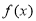 的最小正周期为
的最小正周期为 ,且
,且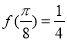 .
.
(1)求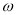 和
和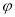 的值;
的值;
(2)求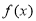 的单调递增区间;
的单调递增区间;
(3)求函数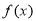 在区间
在区间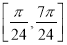 上的最小值和最大值.
上的最小值和最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com