
| 女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 20 | 40 | 80 | 50 | 10 | |
| 男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 频数 | 45 | 75 | 90 | 60 | 30 |
分析 (Ⅰ)求出女性用户和男性用户的频率分布直方图,由图可得女性用户的波动小,男性用户的波动大.
(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,从6人人任取3人,记评分小于90分的人数为X,则X取值为1,2,3,分别求出相应在的概率,由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)女性用户和男性用户的频率分布直方图分别如下左、右图: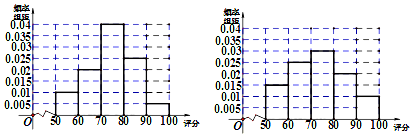
由图可得女性用户的波动小,男性用户的波动大.
(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,
其中评分小于90分的人数为4,从6人人任取3人,
记评分小于90分的人数为X,则X取值为1,2,3,
$P(X=1)=\frac{C_4^1C_2^2}{C_6^3}=\frac{1}{5}$,
$P(X=2)=\frac{C_4^2C_2^1}{C_6^3}=\frac{3}{5}$,
$P(X=3)=\frac{C_4^3C_2^2}{C_6^3}=\frac{1}{5}$.
所以X的分布列为
| X | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
点评 本题考查频率分布直方略产的应用,考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{5}$ | C. | 2$\sqrt{5}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
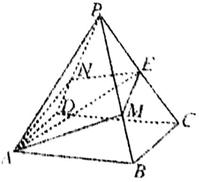 如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC上的点,过AE作平面分别与棱PB、PD交于M、N两点,且$\frac{PM}{PB}$=$\frac{PN}{PD}$=$\frac{2}{3}$.
如图,在正四棱锥P-ABCD中,AB=2,PA=$\sqrt{6}$,E是棱PC上的点,过AE作平面分别与棱PB、PD交于M、N两点,且$\frac{PM}{PB}$=$\frac{PN}{PD}$=$\frac{2}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+$\sqrt{3}$y-2=0 | B. | x+$\sqrt{3}$y-4=0 | C. | $\sqrt{3}$x+y-2=0 | D. | x+$\sqrt{3}$y-6=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
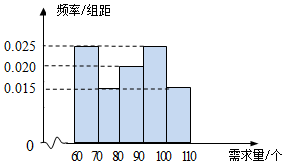 在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.
在某单位的职工食堂中,食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售.如果当天卖不完,剩下的面包以1元/个的价格卖给饲料加工厂.根据以往统计资料,得到食堂每天面包需求量的频率分布直方图如下图所示.食堂某天购进了90个面包,以x(单位:个,60≤x≤110)表示面包的需求量,T(单位:元)表示利润.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 编码方式1 | 编码方式2 | |
| 码元0 |  |  |
| 码元1 |  |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com