
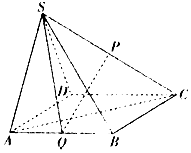
 如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.分析 (1)取SD中点F,连结AF,PF.证明PQ∥AF.利用直线与平面平行的判定定理证明PQ∥平面SAD.
(2)连结BD,证明SE⊥AD.推出SE⊥平面ABCD,得到SE⊥AC.证明EQ⊥AC,然后证明AC⊥平面SEQ,即可证明结论.
解答 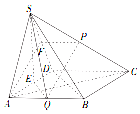 证明:(1)取SD中点F,连结AF,PF.
证明:(1)取SD中点F,连结AF,PF.
∵P,F分别是棱SC,SD的中点,∴FP∥CD,且$FP=\frac{1}{2}CD$,
∵在正方形ABCD中,Q是AB的中点,
∴AQ∥CD,且$AQ=\frac{1}{2}CD$,即FP∥AQ且FP=AQ,
∴AQPF为平行四边形,则PQ∥AF,
∵PQ?平面SAD,AF?平面SAD,∴PQ∥平面SAD.…(6分)
(2)连结BD,∵ABCD是正方形,∴AC⊥BD,
取AD中点E,连SE,EQ,
∵Q为AB中点,∴EQ∥BD,∴AC⊥EQ.
∵SA=SD,∴SE⊥AD,
∵平面SAD⊥平面ABCD,且交线为AD,∴SE⊥平面ABCD,
又AC?平面ABCD,∴AC⊥SE,
∵SE∩EQ=E,SE,EQ?平面SEQ,∴AC⊥平面SEQ,
∵SQ?平面SEQ,∴SQ⊥AC.…(12分)
点评 本题考查直线与平面平行以及直线与平面垂直的判定定理的应用,棱锥的体积的求法,考查计算能力,属于中档题.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
| 立体几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 2和6 | C. | 3和5 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (0,1) | C. | (-∞,1] | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,0) | B. | (-3,6) | C. | (6,2) | D. | (-2,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com