
| A. | (2,0) | B. | (-3,6) | C. | (6,2) | D. | (-2,0) |
分析 设点N的坐标为(x,y),根据平面向量的坐标表示,利用向量相等列方程组,即可求出x、y的值.
解答 解:设点N的坐标为(x,y),
由点M(5,-6)得$\overrightarrow{NM}$=(5-x,-6-y),
又向量$\overrightarrow{a}$=(1,-2),且$\overrightarrow{NM}$=3$\overrightarrow{a}$,
所以$\left\{\begin{array}{l}{5-x=3}\\{-6-y=-6}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$;
所以点N的坐标为(2,0).
故选:A.
点评 本题考查了平面向量的坐标表示与向量相等的应用问题,是基础题目.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
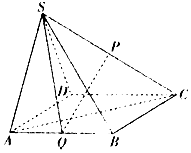 如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,△SAD是正三角形,P,Q分别是棱SC,AB的中点,且平面SAD⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.
某食品厂为了检查甲乙两条自动包装流水线的生产情况,随机在这两条流水线上各抽取40件产品作为样本称出它们的重量(单位:克),重量值落在(495,510]的产品为合格品,否则为不合格品.图1是甲流水线样本的频率分布直方图,表1是乙流水线样本频数分布表.| 产品重量(克) | 频数 |
| (490,495] | 6 |
| (495,500] | 8 |
| (500,505] | 14 |
| (505,510] | 8 |
| (510,515] | 4 |
| 甲流水线 | 乙流水线 | 合计 | |
| 合格品 | a= | b= | |
| 不合格品 | c= | d= | |
| 合 计 | n= |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\frac{3}{2}})$ | B. | $({\frac{3}{2},3})$ | C. | (1,3) | D. | (2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com