
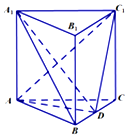
 如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.
如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.分析 (1)连接A1C交AC1于E,利用直三棱柱的性质、矩形的性质、三角形中位线的性质定理即可得到ED∥A1B,再利用线面平行的判定定理即可证明;
(2)建立如图所示空间坐标系D-xyz.利用直线的方向向量和平面的法向量的夹角即可得出线面角.
解答 (1)证明:∵三棱柱ABC-A1B1C1是直三棱柱,∴四边形A1ACC1是矩形.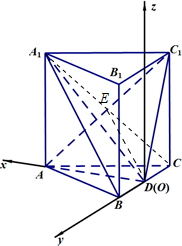
连接A1C交AC1于E,则E是A1C的中点,
又D是BC的中点,在△A1BC中,ED∥A1B.
∵A1B?平面ADC1,ED?平面ADC1,∴A1B∥平面ADC1.
(2)解:∵△ABC是等边三角形,D是BC的中点,∴AD⊥BC.
以D为原点,建立如图所示空间坐标系D-xyz.
令AB=BB1=2,得:D(0,0,0),A($\sqrt{3}$,0,0),
A1($\sqrt{3}$,0,2),C1(0,-1,2).
则$\overrightarrow{DA}$=($\sqrt{3}$,0,0),$\overrightarrow{D{C}_{1}}$=(0,-1,2),
设平面ADC1的法向量为$\overrightarrow{n}$=(x,y,z),
得到$\left\{\begin{array}{l}{\sqrt{3}x=0}\\{-y+2z=0}\end{array}\right.$,令z=1,则x=0,y=2,
∴$\overrightarrow{n}$=(0,2,1)
又$\overrightarrow{D{A}_{1}}$=($\sqrt{3}$,0,2),
∴cos<$\overrightarrow{D{A}_{1}}$,$\overrightarrow{n}$>=$\frac{2}{\sqrt{5}×\sqrt{7}}$=$\frac{2\sqrt{35}}{35}$,
所以A1D与平面ADC1所成角的正弦值为$\frac{2\sqrt{35}}{35}$.
点评 熟练掌握直三棱柱的性质、矩形的性质、三角形中位线的性质定理、线面平行的判定定理、建立空间坐标系利用直线的方向向量和平面的法向量的夹角得出线面角的方法等是解题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数的单调区间可以是函数的定义域 | |
| B. | 函数的多个单调增区间的并集也是其单调增区间 | |
| C. | 具有奇偶性的函数的定义域定关于原点对称 | |
| D. | 关于原点对称的图象一定是奇函数的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
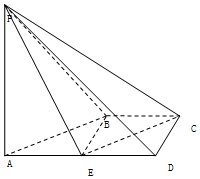 如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为棱AD的中点,异面直线PA与CD所成的角为90°.
如图,在四棱锥P-ABCD中,AD∥BC,∠ADC=∠PAB=90°,BC=CD=$\frac{1}{2}$AD,E为棱AD的中点,异面直线PA与CD所成的角为90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 等腰三角形 | C. | 钝角三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
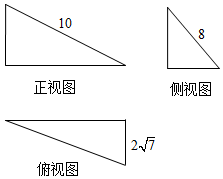
| A. | 32 | B. | $32\sqrt{7}$ | C. | $16\sqrt{7}$ | D. | $64\sqrt{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com