

���� ��I���ɾ�Ҷͼ�е��������������[50��60���ϵ�Ƶ����Ƶ�ʣ��������������
�ټ��������[70��80���ϵ�Ƶ��ֵ��
��II�����ֲ����ԭ�������ó�����֮�ȵ�����ӦƵ��֮�ȣ�
����������γ�ȡ���������æεĿ���ȡֵ�������Ӧ�ĸ���ֵ��д���ֲ��У�
��� �⣺��I���ɾ�Ҷͼ��֪��������[50��60���ϵ�Ƶ��Ϊ4�ˣ�
Ƶ��Ϊ0.008��10=0.08��
��������Ϊ$\frac{4}{0.08}$=50�ˣ�
������[70��80���ϵ�Ƶ��Ϊ
50-��4+14+8+4��=20�ˣ�-------��4�֣�
��II�����ֲ������ԭ�������������γ�����֮�ȵ�����ӦƵ��֮�ȣ�
��[70��80����[80��90����[90��100]������Ƶ��֮�ȵ���5��2��1��
�ɴ˿ɳ�������з�����[70��80������5�ˣ�
������[80��90������2�ˣ�������[90��100]����1�ˣ�
��������֪��=0��1��2��3��
$P����=0��=\frac{C_3^3}{C_8^3}=\frac{1}{56}$��
$P����=1��=\frac{C_3^2C_5^1}{C_8^3}=\frac{15}{56}$��
$P����=2��=\frac{C_3^1C_5^2}{C_8^3}=\frac{15}{28}$��
$P����=3��=\frac{C_5^3}{C_8^3}=\frac{5}{28}$��-------��10�֣�
�ֲ������£�
| �� | 0 | 1 | 2 | 3 |
| p | $\frac{1}{56}$ | $\frac{15}{56}$ | $\frac{15}{28}$ | $\frac{10}{56}$ |
���� ���⿼���˾�Ҷͼ��Ƶ�ʷֲ�ֱ��ͼ����ɢ����������ķֲ������⣬���ۺ��⣮


 ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д� һ��һ��һ��ͨϵ�д�
һ��һ��һ��ͨϵ�д� �㽭֮��ѧҵˮƽ����ϵ�д�
�㽭֮��ѧҵˮƽ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -1 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
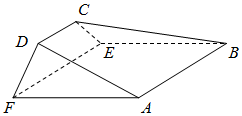 ��ͼ������A��B��C��D��E��FΪ������������У���ABEFΪ���Σ�AF��DF���Ҷ����D-AF-E������C-BE-F������$����0������\frac{��}{2}��$��
��ͼ������A��B��C��D��E��FΪ������������У���ABEFΪ���Σ�AF��DF���Ҷ����D-AF-E������C-BE-F������$����0������\frac{��}{2}��$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
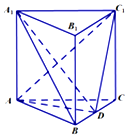 ��ͼ��ֱ������ABC-A1B1C1�У���ABC�ǵȱ������Σ�D��BC���е㣮
��ͼ��ֱ������ABC-A1B1C1�У���ABC�ǵȱ������Σ�D��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 13 | B�� | 14 | C�� | 15 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��С������Ϊ�е��溯�� | B�� | ��С������Ϊ�е�ż���� | ||
| C�� | ��С������Ϊ$\frac{��}{2}$���溯�� | D�� | ��С������Ϊ$\frac{��}{2}$��ż���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com