
【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F.已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE﹣BCF,如图2. 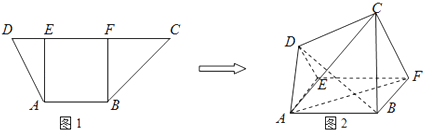
(Ⅰ)若AF⊥BD,证明:△BDE为直角三角形;
(Ⅱ)若DE∥CF, ![]() ,求平面ADC与平面ABFE所成角的余弦值.
,求平面ADC与平面ABFE所成角的余弦值.
【答案】解:证明:连接BE, 由已知可知四边形ABFE是正方形,∴AF⊥BE,
又AF⊥BD,BE∩DE=E,
∴AF⊥平面BDE,又DE平面BDE,
∴AF⊥DE,
又DE⊥AE,AE∩AF=F,
∴DE⊥平面ABFE,又BE平面ABFE,
∴DE⊥BE,即△BDE为直角三角形.
(Ⅱ)取CF的中点M,连结DM,则四边形DEFM是平行四边形,
∴DM=EF=2,CM= ![]() CF=1,又CD=
CF=1,又CD= ![]() ,
,
∴cos∠CMD= ![]() =
= ![]() ,即∠CMD=∠CFE=60°,
,即∠CMD=∠CFE=60°,
过E作EG⊥EF,则EG⊥平面ABFE,
以E为原点,以EA,EF,EG为坐标轴建立空间直角坐标系,
则A(2,0,0),C(0,1, ![]() ),D(0,﹣
),D(0,﹣ ![]() ,
, ![]() ),
),
∴ ![]() =(﹣2,1,
=(﹣2,1, ![]() ),
), ![]() =(﹣2,﹣
=(﹣2,﹣ ![]() ,
, ![]() ),
),
设平面ACD的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 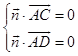 ,
,
即 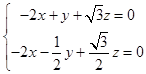 ,令z=
,令z= ![]() 得
得 ![]() =(1,﹣1,
=(1,﹣1, ![]() ),
),
又GE⊥平面ABFE,∴ ![]() =(0,0,1)是平面ABFE的一个法向量,
=(0,0,1)是平面ABFE的一个法向量,
∴cos< ![]() >=
>= ![]() =
= ![]() =
= ![]() ,
,
由图形可知平面ADC与平面ABFE所成角为锐二面角,
∴平面ADC与平面ABFE所成角的余弦值为 ![]() .
.
【解析】(1)由AF⊥BE,AF⊥BD可得AF⊥平面BFE,得出AF⊥DE,结合DE⊥AE即可得出DE⊥平面ABFE,故而DE⊥BE;(2)求出∠CFE的大小,以E为原点建立空间坐标系,求出平面ACD和平面ABFE的法向量,计算两法向量的夹角即可得出二面角的大小.
【考点精析】本题主要考查了直线与平面垂直的性质的相关知识点,需要掌握垂直于同一个平面的两条直线平行才能正确解答此题.


 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 是数列
是数列![]() 的前n项和,
的前n项和,![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)对于正整数![]() ,已知
,已知![]() 成等差数列,求正整数
成等差数列,求正整数![]() 的值;
的值;
(3)设数列![]() 前n项和是
前n项和是![]() ,且满足:对任意的正整数n,都有等式
,且满足:对任意的正整数n,都有等式![]() 成立.求满足等式
成立.求满足等式![]() 的所有正整数n.
的所有正整数n.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如右面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120 km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )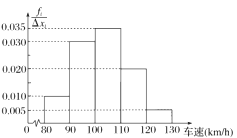
A.30辆
B.1700辆
C.170辆
D.300辆
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过抛物线 ![]() 的焦点,斜率为
的焦点,斜率为 ![]() 的直线交抛物线于
的直线交抛物线于 ![]() ,
, ![]() (
( ![]() )两点,且
)两点,且 ![]() .
.
(1)求该抛物线的方程;
(2)![]() 为坐标原点,
为坐标原点, ![]() 为抛物线上一点,若
为抛物线上一点,若 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季,甲、乙两名篮球运动员都参加了![]() 场比赛,比赛得分情况如下(单位:分)
场比赛,比赛得分情况如下(单位:分)
甲:![]()
乙:![]()

(1)根据得分情况记录,作出两名篮球运动员得分的茎叶图,并根据茎叶图,对甲、乙两运动员得分作比较,写出两个统计结论;
(2)设甲篮球运动员![]() 场比赛得分平均值
场比赛得分平均值![]() ,将
,将![]() 场比赛得分
场比赛得分![]() 依次输入如图所示的程序框图进行运算,问输出的
依次输入如图所示的程序框图进行运算,问输出的![]() 大小为多少?并说明
大小为多少?并说明![]() 的统计学意义;
的统计学意义;
(3)如果从甲、乙两位运动员的![]() 场得分中,各随机抽取一场不少于
场得分中,各随机抽取一场不少于![]() 分的得分,求甲的得分大于乙的得分的概率.
分的得分,求甲的得分大于乙的得分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com