
【题目】做一个无盖的圆柱形水桶,若要使其体积是 ![]() ,且用料最省,则圆柱的底面半径为 .
,且用料最省,则圆柱的底面半径为 .
【答案】3
【解析】设圆柱的高为h,半径为r则由圆柱的体积公式可得,πr2h=27π,即 ![]() ,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh=
,要使用料最省即求全面积的最小值,而S全面积=πr2+2πrh= ![]() =
= ![]()
(法一)令S=f(r),结合导数可判断函数f(r)的单调性,进而可求函数取得最小值时的半径
(法二):S全面积=πr2+2πrh= ![]() =
= ![]() ,利用基本不等式可求用料最小时的r
,利用基本不等式可求用料最小时的r
解:设圆柱的高为h,半径为r
则由圆柱的体积公式可得,πr2h=27π![]()
S全面积=πr2+2πrh= ![]() =
= ![]()
(法一)令S=f(r),(r>0)![]() =
= ![]()
令f′(r)≥0可得r≥3,令f′(r)<0可得0<r<3
∴f(r)在(0,3)单调递减,在[3,+∞)单调递增,则f(r)在r=3时取得最小值
(法二):S全面积=πr2+2πrh= ![]() =
= ![]()
= ![]()
![]() =27π
=27π
当且仅当 ![]() 即r=3时取等号
即r=3时取等号
当半径为3时,S最小即用料最省
故答案为:3
本题主要考查圆柱的体积及表面积的最值问题。要求用料最省,要根据实际问题转化为数学问题,即先设圆柱的高为h,半径为r,根据圆柱的体积公式可得到h,要使用料最省,即求圆柱全面积的最小值,根据公式代入全面积公式,利用不等式即可求解最小值。也可根据导数的单调性求解最小值问题。


科目:高中数学 来源: 题型:
【题目】一个盒子里装有三张卡片,分别标记有数字1,2,3,这三张卡片除标记的数字外完全相同.随机有放回地抽取3次,每次抽取1张,将抽取的卡片上的数字依次记为a,b,c.求:
(1)“抽取的卡片上的数字满足a+b=c”的概率;
(2)“抽取的卡片上的数字a,b,c不完全相同”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某市2017年2月28天的日空气质量指数折线图.
由中国空气质量在线监测分析平台提供的空气质量指数标准如下:
空气质量指数 | (0,50] | (50,100] | (100,150] | (150,200] | (200,300] | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
(Ⅰ)请根据所给的折线图补全如图2所示的频率分布直方图(并用铅笔涂黑矩形区域),并估算该市2月份空气质量指数监测数据的平均数(保留小数点后一位);
(Ⅱ)在该月份中任取两天,求空气质量至少有一天为优或良的概率;
(Ⅲ)如果该市对环境进行治理,治理后经统计,每天的空气质量指数近似满足X~N(75,552),则治理后的空气质量指数均值大约下降了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在高为2的梯形ABCD中,AB∥CD,AB=2,CD=5,过A、B分别作AE⊥CD,BF⊥CD,垂足分别为E、F.已知DE=1,将梯形ABCD沿AE、BF同侧折起,得空间几何体ADE﹣BCF,如图2. 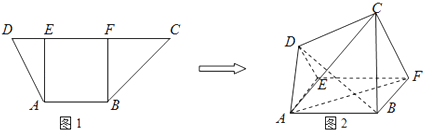
(Ⅰ)若AF⊥BD,证明:△BDE为直角三角形;
(Ⅱ)若DE∥CF, ![]() ,求平面ADC与平面ABFE所成角的余弦值.
,求平面ADC与平面ABFE所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产甲,乙两种产品均需用![]() 两种原料,已知生产1吨每种产品需用
两种原料,已知生产1吨每种产品需用![]() 原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
原料及每天原料的可用限额如下表所示,如果生产1吨甲,乙产品可获利润分别为3万元、4万元,则该企业可获得最大利润为__________万元.
甲 | 乙 | 原料限额 | |
A(吨) | 3 | 2 | 12 |
B(吨) | 1 | 2 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com