Question

14．一长直杆长1.5m，垂直立于底部平坦、水面平静无波的游泳池中，露出水面部分高0.3m，当阳光以与水面成37°的夹角入射时，杆在游泳池底部所成的影长为多少？（已知水的折射率n=$\frac{4}{3}$）

Answer 1

分析 作出光路图，画出棍在水底的影子，由折射率n=$\frac{sinθ}{sinr}$求出折射角，根据几何知识求出影子的长度．

解答 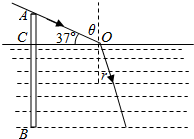解：杆在水中的折射光路图如图所示，影子长为BD．
由题意知：入射角θ=53°，设折射角为r，则根据折射定律n=$\frac{sinθ}{sinr}$，
得：sinr=0.6，cosr=0.8，
则tanr=$\frac{3}{4}$．
故根据几何关系得杆的影长为：
BD=|CO+CB•tanr=0.3×$\frac{4}{3}$+1.2×$\frac{3}{4}$=1.3m．
答：杆AB在水下的影长为1.3m．

点评 本题正确画出光路图是解题的关键之处，作出影子的区域，由折射定律和几何关系结合解题是几何光学常用的方法．