
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病倒数计算,下列各选项中,一定符合上述指标的是( )
①平均数 ![]() ;
;
②标准差S≤2;
③平均数 ![]() 且标准差S≤2;
且标准差S≤2;
④平均数 ![]() 且极差小于或等于2;
且极差小于或等于2;
⑤众数等于1且极差小于或等于1.
A.①②
B.③④
C.③④⑤
D.④⑤
【答案】D
【解析】解:①错.举反倒:0,0,0,0,0,0,7;其平均数 ![]() ,但不符合上述指标;
,但不符合上述指标;
②错.举反倒:7,7,7,7,7,7,7;其标准差S=0≤2,但不符合上述指标;
③错.举反倒:0,3,3,3,3,3,6;其平均数 ![]() 且标准差S≤2,但不符合上述指标;
且标准差S≤2,但不符合上述指标;
④对.若极差小于2,显然符合上述指标;
若极差小于或等于2,有可能(1)0,1,2;(2)1,2,3;(3)2,3,4;(4)3,4,5;(5)4,5,6.
在平均数 ![]() 的条件下,只有(1)(2)(3)成立,符合上述指标;
的条件下,只有(1)(2)(3)成立,符合上述指标;
⑤对.在众数等于1且极差小于或等于1,则最大数不超过5,符合指标.
故选D.
【考点精析】关于本题考查的极差、方差与标准差,需要了解标准差和方差越大,数据的离散程度越大;标准差和方程为0时,样本各数据全相等,数据没有离散性;方差与原始数据单位不同,解决实际问题时,多采用标准差才能得出正确答案.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】【江西省临川实验学校2017届高三第一次模拟考试数学(文)】已知抛物线![]() ,焦点为
,焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() 到
到![]() 的距离比
的距离比![]() 到直线
到直线![]() 的距离小1.
的距离小1.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 与
与![]() ,切点分别为
,切点分别为![]() ,求证:直线
,求证:直线![]() 恒过某一定点.
恒过某一定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,
的图像在点M(-1,f(-1))处的切线方程为x+2y+5=0,
(1)求函数y=f(x)的解析式;
(2)求函数y=f(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点,求
两个不同的点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一辆汽车从![]() 市出发沿海岸一条笔直公路以每小时
市出发沿海岸一条笔直公路以每小时![]() 的速度向东均速行驶,汽车开动时,在
的速度向东均速行驶,汽车开动时,在![]() 市南偏东方向距
市南偏东方向距![]() 市
市![]() 且与海岸距离为
且与海岸距离为![]() 的海上
的海上![]() 处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
处有一快艇与汽车同时出发,要把一份稿件交给这汽车的司机.
(1)快艇至少以多大的速度行驶才能把稿件送到司机手中?
(2)在(1)的条件下,求快艇以最小速度行驶时的行驶方向与![]() 所成的角.
所成的角.

查看答案和解析>>
科目:高中数学 来源: 题型:
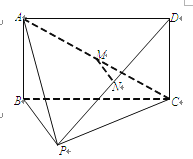
【题目】如图,在四棱锥P-ABCD中,四边形ABCD为矩形,AB⊥BP,M为AC的中点,N为PD上一点.
(1)若MN∥平面ABP,求证:N为PD的中点;
(2)若平面ABP⊥平面APC,求证:PC⊥平面ABP.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设两个非零向量 ![]() 和
和 ![]() 不共线.
不共线.
(1)如果 ![]() =
= ![]() +
+ ![]() ,
, ![]() =2
=2 ![]() +8
+8 ![]() ,
, ![]() =3
=3 ![]() ﹣3
﹣3 ![]() ,求证:A、B、D三点共线;
,求证:A、B、D三点共线;
(2)若| ![]() |=2,|
|=2,| ![]() |=3,
|=3, ![]() 与
与 ![]() 的夹角为60°,是否存在实数m,使得m
的夹角为60°,是否存在实数m,使得m ![]() +
+ ![]() 与
与 ![]() ﹣
﹣ ![]() 垂直?并说明理由.
垂直?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的短轴长为
的短轴长为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上异于左、右顶点
上异于左、右顶点![]() 的一点.
的一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:点
,证明:点![]() 关于直线
关于直线![]() 的对称点在直线
的对称点在直线![]() 上.
上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com