已知数列{an}的前n项和为Sn,且有a1=2,Sn=2an-2.
(I)求数列{an}的通项公式;
(Ⅱ)若bn=n•an,求数列{bn}的前n项和Tn.
解:(Ⅰ)∵S
n=2a
n-2,∴S
n-1=2a
n-1-2(n≥2),
∴a
n=2a
n-1,∴
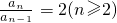
,
又∵a
1=2,∴{a
n}是以2为首项,2为公比的等比数列,
∴
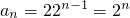
. …(5分)
(Ⅱ)
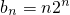
,
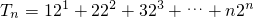
,
∴
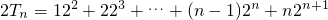
.
两式相减得:
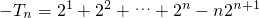
,
∴

=(1-n)•2
n+1-2,
∴
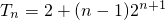
. …(12分)
分析:(Ⅰ)利用数列递推式,再写一式,两式相减,可得{a
n}是以2为首项,2为公比的等比数列,即可求得数列的通项公式;
(Ⅱ)利用错位相减法,可求数列{b
n}的前n项和T
n.
点评:本题考查数列递推式,考查等比数列的判断,考查数列的通项与求和,考查学生的计算能力,属于中档题.
