
(12分)已知椭圆C: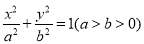 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 与以椭圆C的右焦点为圆心,以
与以椭圆C的右焦点为圆心,以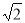
 为半径的圆相切.
为半径的圆相切.
(1)求椭圆的方程.
(2)若过椭圆 的右焦点
的右焦点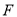 作直线
作直线 交椭圆
交椭圆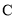 于
于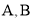 两点,交y轴于
两点,交y轴于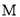 点,且
点,且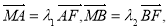 求证:
求证: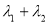 为定值
为定值
(1)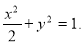 ,(2)
,(2)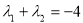
【解析】
试题分析:(1)由题意圆的方程可设为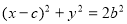 ,利用圆心到直线的距离为
,利用圆心到直线的距离为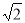
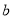 再由焦点与短轴的一个端点的连线构成等腰直角三角形即b=c即可解决;(2)与圆锥曲线相关的最值、范围问题综合性较强,解决的思路有两种:一是由题目中的限制条件求范围,如直线与圆锥曲线的位置关系中Δ的范围,方程中变量的范围,角度的大小等;二是将要讨论的几何量如长度、面积、代数式等用参数表示出来,再对表达式进行讨论,应用不等式、三角函数等知识求最值,在解题过程中注意向量,不等式的应用
再由焦点与短轴的一个端点的连线构成等腰直角三角形即b=c即可解决;(2)与圆锥曲线相关的最值、范围问题综合性较强,解决的思路有两种:一是由题目中的限制条件求范围,如直线与圆锥曲线的位置关系中Δ的范围,方程中变量的范围,角度的大小等;二是将要讨论的几何量如长度、面积、代数式等用参数表示出来,再对表达式进行讨论,应用不等式、三角函数等知识求最值,在解题过程中注意向量,不等式的应用
试题解析:(1)由题意:以椭圆C的右焦点为圆心,以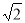
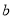 为半径的圆的方程为
为半径的圆的方程为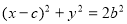 ,
,
∴圆心到直线 的距离
的距离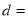
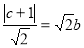 ①
①
∵椭圆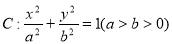 的两焦点与短轴的一个端点的连线构成等腰直角三角形, b=c,代入①式得b=1
的两焦点与短轴的一个端点的连线构成等腰直角三角形, b=c,代入①式得b=1
∴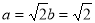 故所求椭圆方程为
故所求椭圆方程为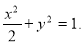 4分
4分
(2)由题意:直线 的斜率存在,所以设直线
的斜率存在,所以设直线 方程为
方程为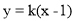 ,则
,则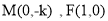
将直线方程代入椭圆方程得: 6分
6分
设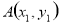 ,
,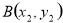 则
则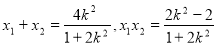 ① 8分
① 8分
由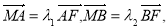 ∴
∴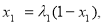
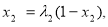
即: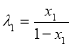
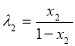 10分
10分
 =
=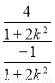 =-4 ∴
=-4 ∴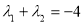 12分
12分
考点:椭圆及其综合应用


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年河南省高二上学期第一次月考试理科数学卷(解析版) 题型:选择题
已知数列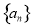 满足
满足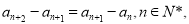 且
且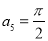 若函数
若函数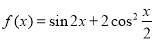 ,记
,记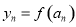 则数列
则数列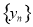 的前9项和为( )
的前9项和为( )
A.0 B.-9 C.9 D.1
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河南省高二上学期第一次月考试理科数学卷(解析版) 题型:选择题
在△ABC中,已知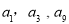 ,则角A=( )
,则角A=( )
A.30°或150° B.60°或120° C.60° D.30°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北邢台一中高二上学期期中考试文科数学试卷(解析版) 题型:解答题
(10分)已知双曲线的中心在坐标原点,焦点在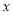 轴上,实轴长是虚轴长的2倍,且过点
轴上,实轴长是虚轴长的2倍,且过点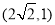 , 求双曲线的标准方程及离心率.
, 求双曲线的标准方程及离心率.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北邢台一中高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知双曲线 的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )
的右焦点为F,若过点F的直线与双曲线的右支有且只有一个交点,则此直线的斜率的取值范围是( )
A. B.
B.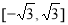 C.
C. D.
D.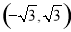
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考文科数学试卷(解析版) 题型:填空题
如图所示,在△ABC中,AD是高线, 是中线, DC=BE, DG
是中线, DC=BE, DG CE于G, EC的长为8,
CE于G, EC的长为8,
则EG=__________________.

查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:填空题
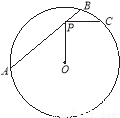
(几何证明选讲)如图,点P为圆O的弦AB上的一点,连接PO,过点P作PC?OP,且PC交圆O于C. 若AP=4,PC=2,则PB= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com