
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点,以
边的中点,以![]() 为折痕把
为折痕把![]() 折起,使点
折起,使点![]() 到达点
到达点![]() 的位置,且
的位置,且![]() .
.
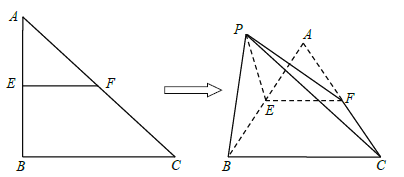
(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由![]() ,
,![]() 分别为
分别为![]() ,
,![]() 边的中点,可得
边的中点,可得![]() ,由已知结合线面垂直的判定可得
,由已知结合线面垂直的判定可得![]() 平面
平面![]() ,从而得到
,从而得到![]() 平面
平面![]() ;(2)取
;(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由已知证明
,由已知证明![]() 平面
平面![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,分别以
,分别以![]() ,
,![]() ,
,![]() 所在直线为
所在直线为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,分别求出平面
轴建立空间直角坐标系,分别求出平面![]() 与平面
与平面![]() 的一个法向量,由两法向量所成角的余弦值可得平面
的一个法向量,由两法向量所成角的余弦值可得平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)因为![]() 分别为
分别为![]() ,
,![]() 边的中点,
边的中点,
所以![]() ,
,
因为![]() ,
,
所以![]() ,
,![]() ,
,
又因为![]() ,
,
所以![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
由(1)知![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,
,
因为![]() ,
,
所以![]() ,
,
又因为![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
,
过![]() 作
作![]() 交
交![]() 于
于![]() ,分别以
,分别以![]() ,
,![]() ,
,![]() 所在直线为
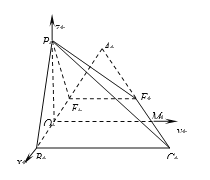
所在直线为![]() 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则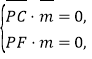 即
即![]()
则![]() ,
,
易知![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
![]() ,
,
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值
所成锐二面角的余弦值![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】对 n N ,设抛物线 y2 2(2n 1) x ,过 P 2n, 0 任作直线 l 与抛物线交与 An, Bn两点,则数列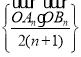 的前 n 项和为_____;
的前 n 项和为_____;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行促销活动,有两个摸奖箱,![]() 箱内有一个“
箱内有一个“![]() ”号球、两个“
”号球、两个“![]() ”号球、三个“
”号球、三个“![]() ”号球、四个无号球,
”号球、四个无号球,![]() 箱内有五个“
箱内有五个“![]() ”号球、五个“
”号球、五个“![]() ”号球,每次摸奖后放回,消费额满
”号球,每次摸奖后放回,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,消费额满
箱内摸奖机会,消费额满![]() 元有一次
元有一次![]() 箱内摸奖机会,摸得有数字的球则中奖,“
箱内摸奖机会,摸得有数字的球则中奖,“![]() ”号球奖
”号球奖![]() 元、“
元、“![]() ”号球奖
”号球奖![]() 元、“
元、“![]() ”号球奖
”号球奖![]() 元,摸得无号球则没有奖金.
元,摸得无号球则没有奖金.
(Ⅰ)经统计,消费额![]() 服从正态分布
服从正态分布![]() ,某天有
,某天有![]() 为顾客,请估计消费额
为顾客,请估计消费额![]() (单位:元)在区间
(单位:元)在区间![]() 内并中奖的人数;
内并中奖的人数;
(Ⅱ)某三位顾客各有一次![]() 箱内摸奖机会,求其中中奖人数
箱内摸奖机会,求其中中奖人数![]() 的分布列;
的分布列;
(Ⅲ)某顾客消费额为![]() 元,有两种摸奖方法,方法一:三次
元,有两种摸奖方法,方法一:三次![]() 箱内摸奖机会;方法二:一次
箱内摸奖机会;方法二:一次![]() 箱内摸奖机会,请问:这位顾客选哪一种方法所得奖金的期望值较大.
箱内摸奖机会,请问:这位顾客选哪一种方法所得奖金的期望值较大.
附:若![]() ,则
,则![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线l1:2x-y+a=0(a>0),直线l2:4x-2y-1=0和直线l3:x+y-1=0,且l1和l2的距离是![]() .
.
(1)求a的值.
(2)能否找到一点P,使得P点同时满足下列三个条件:①P是第一象限的点;②P点到l1的距离是P点到l2的距离的![]() ;③P点到l1的距离与P点到l3的距离之比是
;③P点到l1的距离与P点到l3的距离之比是![]() ?若能,求出P点坐标;若不能,请说明理由.
?若能,求出P点坐标;若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,将一块直角三角形板![]() 置于平面直角坐标系中,已知
置于平面直角坐标系中,已知![]() ,点
,点![]() 是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点
是三角板内一点,现因三角板中,阴影部分受到损坏,要把损坏部分锯掉,可用经过点![]() 的任一直线
的任一直线![]() 将三角板锯成
将三角板锯成![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() .
.
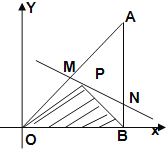
(1)用![]() 表示出直线
表示出直线![]() 的方程,并求出点
的方程,并求出点![]() 的坐标;
的坐标;
(2)求出![]() 的取值范围及其所对应的倾斜角
的取值范围及其所对应的倾斜角![]() 的范围;
的范围;
(3)求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是双曲线
是双曲线![]() 的左右焦点,其渐近线为
的左右焦点,其渐近线为![]() ,且其右焦点与抛物线
,且其右焦点与抛物线![]() 的焦点
的焦点![]() 重合.
重合.
(1)求双曲线![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 的法向量为
的法向量为![]() ,且
,且![]() ,求
,求![]() 的值
的值
(3)在(2)的条件下,若双曲线![]() 在第四象限的部分存在一点
在第四象限的部分存在一点![]() 满足
满足![]() ,求
,求![]() 的值及
的值及![]() 的面积
的面积![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个生产公司投资A生产线500万元,每万元可创造利润![]() 万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了
万元,该公司通过引进先进技术,在生产线A投资减少了x万元,且每万元的利润提高了![]() ;若将少用的x万元全部投入B生产线,每万元创造的利润为
;若将少用的x万元全部投入B生产线,每万元创造的利润为![]() 万元,其中
万元,其中![]() .
.
![]() 若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
若技术改进后A生产线的利润不低于原来A生产线的利润,求x的取值范围;
![]() 若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
若生产线B的利润始终不高于技术改进后生产线A的利润,求a的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的值域为
的值域为![]() ,记函数
,记函数![]() .
.
(1)求实数![]() 的值;
的值;
(2)存在![]() 使得不等式
使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 有5个不等的实数根,求实数
有5个不等的实数根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com