
【题目】已知圆![]() :
:![]() (
(![]() ),定点
),定点![]() ,
,![]() ,其中
,其中![]() 为正实数.
为正实数.
(1)当![]() 时,判断直线
时,判断直线![]() 与圆
与圆![]() 的位置关系;
的位置关系;
(2)当![]() 时,若对于圆
时,若对于圆![]() 上任意一点
上任意一点![]() 均有
均有![]() 成立(
成立(![]() 为坐标原点),求实数
为坐标原点),求实数![]() 的值;
的值;
(3)当![]() 时,对于线段
时,对于线段![]() 上的任意一点
上的任意一点![]() ,若在圆
,若在圆![]() 上都存在不同的两点
上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求实数
的中点,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 相离. (2) ![]() ,
,![]() .(3)
.(3) ![]()
【解析】
(1)利用圆心到直线的距离和半径的关系即可得到判断;(2)利用两点间的距离公式进行化简整理,由点P的任意性即可得实数m,λ的值;(3)设出点P和点N的坐标,表示出中点M的坐标,M、N满足圆C的方程,根据方程组有解说明两圆有公共点,利用两圆位置关系要求及点P满足直线AB的方程,解出半径的取值范围.
解: (1) 当![]() 时,圆心为
时,圆心为![]() ,半径为
,半径为![]() ,
,
当![]() 时,直线
时,直线![]() 方程为
方程为![]() ,
,
所以,圆心到直线距离为![]() ,
,
因为![]() ,所以,直线与圆相离.
,所以,直线与圆相离.
(2)设点![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
![]() ,…………
,…………
由![]() 得,
得,![]() , ∴
, ∴![]() ,
,
代入得, ![]() ,
,
化简得![]() ,…………
,…………
因为![]() 为圆
为圆![]() 上任意一点
上任意一点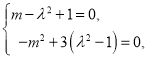 ………
………
又![]() ,解得
,解得![]() ,
,![]() .…………………
.…………………
(3)法一:直线![]() 的方程为
的方程为![]() ,设
,设![]() (
(![]() ),
),![]() ,
,
因为点![]() 是线段
是线段![]() 的中点,所以
的中点,所以![]() ,
,
又![]() 都在圆
都在圆![]() :
:![]() 上,所以
上,所以
即 ……………………
……………………
因为该关于![]() 的方程组有解,即以
的方程组有解,即以![]() 为圆心,
为圆心,![]() 为半径的圆与以
为半径的圆与以![]() 为圆心,
为圆心,![]() 为半径的圆有公共点,
为半径的圆有公共点,
所以,![]() ,
,
又![]() 为线段
为线段![]() 上的任意一点,所以
上的任意一点,所以![]() 对所有
对所有![]() 成立.
成立.
而![]()
![]() 在
在![]() 上的值域为
上的值域为![]() ,
,
所以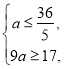 所以
所以![]() .………
.………
又线段![]() 与圆
与圆![]() 无公共点,所以
无公共点,所以![]() ,∴
,∴![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() . ……………
. ……………
法二:过圆心![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,设
,设![]() ,
,![]() ,则
,则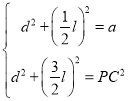 则消去
则消去![]() 得,
得, ![]() ,
,![]()
![]()
![]() 直线
直线![]() 方程为
方程为![]()
![]() 点
点![]() 到直线
到直线![]() 的距离为
的距离为![]()
且![]() 又
又![]()
![]() 为线段
为线段![]() 上的任意一点,
上的任意一点,![]()
![]() …
…
![]() ,
,![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】某企业甲,乙两个研发小组,他们研发新产品成功的概率分别为![]() 和
和![]() ,现安排甲组研发新产品
,现安排甲组研发新产品![]() ,乙组研发新产品
,乙组研发新产品![]() .设甲,乙两组的研发是相互独立的.
.设甲,乙两组的研发是相互独立的.
(1)求至少有一种新产品研发成功的概率;
(2)若新产品![]() 研发成功,预计企业可获得
研发成功,预计企业可获得![]() 万元,若新产品
万元,若新产品![]() 研发成功,预计企业可获得利润
研发成功,预计企业可获得利润![]() 万元,求该企业可获得利润的分布列和数学期望.
万元,求该企业可获得利润的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左右焦点为
的左右焦点为![]() ,
,![]() ,
,![]() 是椭圆上半部分的动点,连接
是椭圆上半部分的动点,连接![]() 和长轴的左右两个端点所得两直线交
和长轴的左右两个端点所得两直线交![]() 正半轴于
正半轴于![]() ,
,![]() 两点(点
两点(点![]() 在
在![]() 的上方或重合).
的上方或重合).
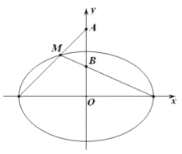
(1)当![]() 面积
面积![]() 最大时,求椭圆的方程;
最大时,求椭圆的方程;
(2)当![]() 时,若
时,若![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的方程;
的方程;
(3)当![]() 时,在
时,在![]() 轴上是否存在点
轴上是否存在点![]() 使得
使得![]() 为定值,若存在,求
为定值,若存在,求![]() 点的坐标,若不存在,说明理由.
点的坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把半椭圆![]() (
(![]() )与圆弧
)与圆弧![]() (
(![]() )合成的曲线称作“曲圆”,其中
)合成的曲线称作“曲圆”,其中![]() 为
为![]() 的右焦点,如图所示,
的右焦点,如图所示,![]() 、
、![]() 、
、![]() 、
、![]() 分别是“曲圆”与
分别是“曲圆”与![]() 轴、
轴、![]() 轴的交点,已知
轴的交点,已知![]() ,过点
,过点![]() 且倾斜角为
且倾斜角为![]() 的直线交“曲圆”于
的直线交“曲圆”于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 轴的上方).
轴的上方).
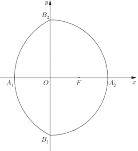
(1)求半椭圆![]() 和圆弧
和圆弧![]() 的方程;
的方程;
(2)当点![]() 、
、![]() 分别在第一、第三象限时,求△
分别在第一、第三象限时,求△![]() 的周长
的周长![]() 的取值范围;
的取值范围;
(3)若射线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 交“曲圆”于点
交“曲圆”于点![]() ,请用
,请用![]() 表示
表示![]() 、
、![]() 两点的坐标,并求△
两点的坐标,并求△![]() 的面积的最小值.
的面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x![]() y
y![]() 2=0,抛物线C:y2=2px(p>0).
2=0,抛物线C:y2=2px(p>0).
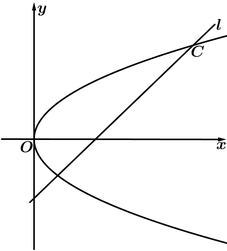
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为![]() ;
;
②求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市春节期间7家超市的广告费支出![]() (万元)和销售额
(万元)和销售额![]() (万元)数据如下:
(万元)数据如下:
超市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)用二次函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程:
的关系,可得回归方程:![]() ,
,
经计算二次函数回归模型和线性回归模型的![]() 分别约为
分别约为![]() 和
和![]() ,请用
,请用![]() 说明选择哪个回归模型更合适,并用此模型预测
说明选择哪个回归模型更合适,并用此模型预测![]() 超市广告费支出为3万元时的销售额.
超市广告费支出为3万元时的销售额.
参数数据及公式:![]() ,
,![]() ,
,
 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,计算得
(单位:千元)的数据资料,计算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 关于月收入
关于月收入![]() 的线性回归方程
的线性回归方程![]() ,并判断变量
,并判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.(注:线性回归方程![]() 中,
中,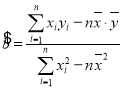 ,其中
,其中![]() ,
,![]() 为样本平均值.)
为样本平均值.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com