
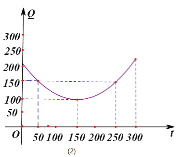
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场销售价与上市时间的关系用图(1)的一条折线表示;西红柿的种植成本与上市时间的关系用图(2)的抛物线段表示.
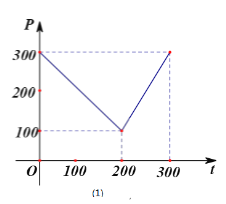
(1)写出图(1)表示的市场售价与时间的函数关系式![]() ;写出图(2)表示的种植成本与时间的函数关系式
;写出图(2)表示的种植成本与时间的函数关系式![]() ;
;
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?(注:市场售价和种植成本的单位:元/![]() kg,时间单位:天.)
kg,时间单位:天.)
【答案】(1)![]() ;
;![]() ;(2)从2月1日开始的第50天时,上市的西红柿纯收益最大
;(2)从2月1日开始的第50天时,上市的西红柿纯收益最大
【解析】
(1)根据函数图象可知![]() 为分段函数,每一段均为依次函数;
为分段函数,每一段均为依次函数;![]() 为二次函数;由函数图象所过点即可求得函数解析式;
为二次函数;由函数图象所过点即可求得函数解析式;
(2)令![]() ,得到函数解析式,纯收益最大即为
,得到函数解析式,纯收益最大即为![]() 最大;分别在
最大;分别在![]() 和
和![]() 两种情况下,结合二次函数性质确定最大值点和最大值,综合可得最终结论.
两种情况下,结合二次函数性质确定最大值点和最大值,综合可得最终结论.
(1)由图(1)可得市场售价与时间的函数关系为![]()
由图(2)可得种植成本与时间的函数关系为![]()
(2)设![]() 时刻的纯收益为
时刻的纯收益为![]() ,则
,则![]()
即
当![]() 时,配方得到
时,配方得到![]()
![]() 当
当![]() 时,
时,![]() 取得区间
取得区间![]() 上的最大值为
上的最大值为![]() ;
;
当![]() 时,配方整理得到:
时,配方整理得到:![]()
![]() 当
当![]() 时,
时,![]() 取得区间
取得区间![]() 上的最大值为
上的最大值为![]()
综上所述,![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,此时
,此时![]()
即从![]() 月
月![]() 日开始的第
日开始的第![]() 天时,上市的西红柿纯收益最大
天时,上市的西红柿纯收益最大


科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]()
(1)若4比![]() 接近0,求
接近0,求![]() 的取值范围;
的取值范围;
(2)对于任意的两个不等正数![]() ,求证:
,求证:![]() 比
比![]() 接近
接近![]() ;
;
(3)若对于任意的非零实数![]() ,实数
,实数![]() 比
比![]() 接近
接近![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是枇把生产大国,在对枇杷的长期栽培和选育中,形成了众多的品种.成熟的枇杷味道甜美,营养颇丰,而且中医认为枇杷有润肺、止咳、止渴的功效.因此,枇杷受到大家的喜爱.某果农调查了枇杷上市时间与卖出数量的关系,统计如表所示:

结合散点图可知,![]() 线性相关.
线性相关.
(Ⅰ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() =
=![]()
![]() (其中
(其中![]() ,
,![]() 用假分数表示);
用假分数表示);
(Ⅱ)计算相关系数![]() ,并说明(I)中线性回归模型的拟合效果.
,并说明(I)中线性回归模型的拟合效果.
参考数据:![]() ;
;
参考公式:回归直线方程![]() =
=![]()
![]() 中的斜率和截距的最小二乘法估计公式分别为:
中的斜率和截距的最小二乘法估计公式分别为:
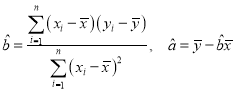 ;相关系数
;相关系数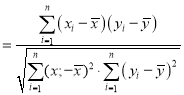
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件,求圆的标准方程:
(1)已知点A(1,1),B(﹣1,3),且AB是圆的直径,求圆的标准方程;
(2)圆与y轴交于A(0,﹣4),B(0,﹣2),圆心在直线2x﹣y﹣7=0上,求圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说:“你们四人中有![]() 位优秀,
位优秀,![]() 位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.”看后甲对大家说:“我还是不知道我的成绩.”根据以上信息,则( )
位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.”看后甲对大家说:“我还是不知道我的成绩.”根据以上信息,则( )
A.乙可以知道两人的成绩B.丁可能知道两人的成绩
C.乙、丁可以知道自己的成绩D.乙、丁可以知道对方的成绩
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 .直线
.直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 、
、![]() 、
、![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com