【题目】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说：“你们四人中有
位优秀，位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩.”看后甲对大家说：“我还是不知道我的成绩.”根据以上信息，则（ ）
A.乙可以知道两人的成绩B.丁可能知道两人的成绩
C.乙、丁可以知道自己的成绩D.乙、丁可以知道对方的成绩
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某蔬菜基地种植西红柿，由历年市场行情得知，从二月一日起的300天内，西红柿市场销售价与上市时间的关系用图（1）的一条折线表示；西红柿的种植成本与上市时间的关系用图（2）的抛物线段表示.
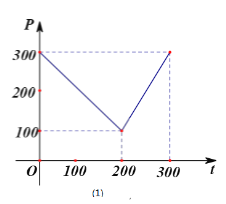
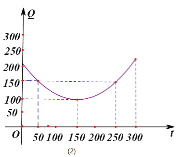
（1）写出图（1）表示的市场售价与时间的函数关系式
；写出图（2）表示的种植成本与时间的函数关系式
；
（2）认定市场售价减去种植成本为纯收益，问何时上市的西红柿收益最大？（注：市场售价和种植成本的单位：元/
kg，时间单位：天.）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
、
、
表示不同的直线，
、
、
表示不同的平面，给出下列
个命题：其中命题正确的个数是（ ）
①若
，且
，则
；
②若，且
，则
；
③若
，
，
，则
；
④ 若，，，且
，则.
A.
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为：
（
为参数），在以
为极点，
轴正半轴为极轴的极坐标系中，曲线
的极坐标方程为
.
（1）求曲线的普通方程和曲线的直角坐标方程；
（2）若曲线与交于
，
两点，点
的坐标为
，求
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
为矩形，平面
平面
，
，
，
为
的中点..
（1）求证：平面
平面
；
（2）
，在线段
上是否存在一点
，使得二面角
的余弦值为
.请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝sin ωx·cos ωx＋
cos2ωx－
(ω＞0)，直线x＝x1，x＝x2是y＝f(x)图象的任意两条对称轴，且|x1－x2|的最小值为
.
（Ⅰ）求f(x)的表达式；
（Ⅱ）将函数f(x)的图象向右平移
个单位长度后，再将得到的图象上各点的横坐标伸长为原来的2倍，纵坐标不变，得到函数y＝g(x)的图象，求函数g(x)的单调减区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
