
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为:
的参数方程为: (
(![]() 为参数),在以
为参数),在以![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 的坐标为
的坐标为![]() ,求
,求![]() .
.
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:
【题目】若实数![]() 满足
满足![]() ,则称
,则称![]() 比
比![]() 接近
接近![]()
(1)若4比![]() 接近0,求
接近0,求![]() 的取值范围;
的取值范围;
(2)对于任意的两个不等正数![]() ,求证:
,求证:![]() 比
比![]() 接近
接近![]() ;
;
(3)若对于任意的非零实数![]() ,实数
,实数![]() 比
比![]() 接近
接近![]() ,求
,求![]() 的取值范围
的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下列条件,求圆的标准方程:
(1)已知点A(1,1),B(﹣1,3),且AB是圆的直径,求圆的标准方程;
(2)圆与y轴交于A(0,﹣4),B(0,﹣2),圆心在直线2x﹣y﹣7=0上,求圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩,老师说:“你们四人中有![]() 位优秀,
位优秀,![]() 位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.”看后甲对大家说:“我还是不知道我的成绩.”根据以上信息,则( )
位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.”看后甲对大家说:“我还是不知道我的成绩.”根据以上信息,则( )
A.乙可以知道两人的成绩B.丁可能知道两人的成绩
C.乙、丁可以知道自己的成绩D.乙、丁可以知道对方的成绩
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《福建省高考改革试点方案》规定:从2018年秋季高中入学的新生开始,不分文理科;2021年开始,高考总成绩由语数外3门统考科目和物理、化学等六门选考科目构成,将每门选考科目的考生原始成绩从高到低划分为A、B+、B、C+、C、D+、D、E共8个等级,参照正态分布原则,确定各等级人数所占比例分别为3%、7%、18%、22%、22%、18%、7%、3%,选考科目成绩计入考生总成绩时,将A至E等级内的考生原始成绩,依照等比例转换法则,分别转换到[91,100]、[81,90]、[71.80]、[61,70]、[51,60]、[41,50]、[31,40]、[21,30]八个分数区间,得到考生的等级成绩,某校高一年级共2000人,为给高一学生合理选科提供依据,对六门选考科目进行测试,其中化学考试原始成绩![]() 基本服从正态分布
基本服从正态分布![]() .
.
(1)求化学原始成绩在区间(57,96)的人数;
(2)以各等级人数所占比例作为各分数区间发生的概率,按高考改革方案,若从全省考生中随机抽取3人,记![]() 表示这3人中等级成绩在区间[71,90]的人数,求事件
表示这3人中等级成绩在区间[71,90]的人数,求事件![]() 的概率
的概率
(附:若随机变量![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.

(1)求证:平面PAC⊥平面PBC;
(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 如图,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,
,![]() 分别为
分别为![]() 的中点,沿
的中点,沿![]() 将
将![]() 折起,得到如图所示的四棱锥
折起,得到如图所示的四棱锥![]()

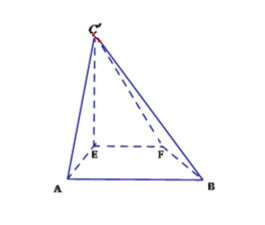
(1)求证:![]() 平面
平面![]() ;
;
(2)当四棱锥![]() 体积取最大值时,
体积取最大值时,
(i) 写出最大体积;
(ii) 求![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为 .直线
.直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 、
、![]() 、
、![]() 成等比数列,求实数
成等比数列,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某机械厂欲从![]() 米,
米,![]() 米的矩形铁皮中裁剪出一个四边形
米的矩形铁皮中裁剪出一个四边形![]() 加工成某仪器的零件,裁剪要求如下:点
加工成某仪器的零件,裁剪要求如下:点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
,![]() .设
.设![]() ,四边形
,四边形![]() 的面积为
的面积为![]() (单位:平方米).
(单位:平方米).

(1)求![]() 关于
关于![]() 的函数关系式,求出定义域;
的函数关系式,求出定义域;
(2)当![]() 的长为何值时,裁剪出的四边形
的长为何值时,裁剪出的四边形![]() 的面积最小,并求出最小值.
的面积最小,并求出最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com