练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．在△ABC中，角A，B，C所对的边分别为a，b，c，若$\sqrt{3}acosB+bsinA=0$，则B=（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{2π}{3}$D．$\frac{5π}{6}$

    分析 根据条件和正弦定理得出tanB，得出B．

    解答 解：在△ABC中，∵$\sqrt{3}acosB+bsinA=0$，∴$\frac{a}{sinA}=\frac{b}{-\sqrt{3}cosB}$，
    又∵$\frac{a}{sinA}=\frac{b}{sinB}$，
    ∴sinB=-$\sqrt{3}$cosB，
    ∴tanB=-$\sqrt{3}$．
    ∴B=$\frac{2π}{3}$．
    故选：C．

    点评 本题考查了正弦定理，特殊角的三角函数值，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤0}\\{{-x}^{2}，x＞0}\end{array}\right.$，不等式f（ax2）+f（1-ax）＜0对任意的x∈R都成立，则实数a的取值范围（　　）
    A．（0，4）B．（-4，0）C．[0，4）D．[0，4]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．复数$\frac{3-i}{i}$=（　　）
    A．1+3iB．-1-3iC．-1+3iD．1-3i

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目．以普通人讲述手中账单背后的故事，并参与因此而量身为其定制的大型游戏，来赢得账单报销的形式，讲述了人与人之间的真情，展现了当今百姓生活中的万般幸福之态．某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究，由此得到如下频数分布表：
    报账人的账单总额（元）[0，1000）[1000，2000）[2000，3000）[3000，4000）[4000，5000）[5000，6000）
     频数 2412 32 10 14 8
    （Ⅰ）在如表中作出这些数据的频率分布直方图：
    （Ⅱ）若将频率视为概率，从参与节目的报账人中随机抽取3位（看作有放回的抽样），求账单总额在[3000，4000）内的报账人数X的分布列、数学期望、与方差．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

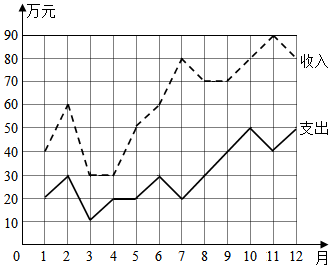
    17．某工厂一年中各月份的收入、支出情况的统计如图所示，下列说法中错误的是（　　）

    （注：结余=收入-支出）
    A．收入最高值与收入最低值的比是3：1
    B．结余最高的月份是7月
    C．1至2月份的收入的变化率与4至5月份的收入的变化率相同
    D．前6个月的平均收入为40万元

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知函数$f（x）=\frac{k+x}{k-x}•{e^x}$（k∈R）．
    （Ⅰ）若k=1，求曲线y=f（x）在点（0，f（0））处的切线方程；
    （Ⅱ）求函数f（x）的单调区间；
    （Ⅲ）设k≤0，若函数f（x）在区间$（{\sqrt{3}，2\sqrt{2}}）$上存在极值点，求k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在等比数列{an}中，${a_1}+{a_2}=\frac{1}{2}，{a_5}+{a_6}=8，{a_n}＞0$，则a3+a4=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知$\overrightarrow{a}$，$\overrightarrow{b}$是不共线的两个向量，且$\overrightarrow{a}$$•\overrightarrow{b}$＞0，|$\overrightarrow{b}$|≥4，若对任意m，n∈R，|$\overrightarrow{a}$+m$\overrightarrow{b}$|的最小值是1，|$\overrightarrow{b}$+n$\overrightarrow{a}$|的最小值是2，则$\overrightarrow{a}$$•\overrightarrow{b}$的最小值是4$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．已知椭圆M：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点分别为F1、F2，点A是椭圆M与圆C：x2+（y-2$\sqrt{2}$b）2=$\frac{4}{9}$m2在第一象限的交点，且点A到F2的距离等于$\frac{1}{3}$m，若椭圆M上一动点到点F1与到点C的距离之差的最大值为2a-m，则椭圆M的离心率为$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案