
 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
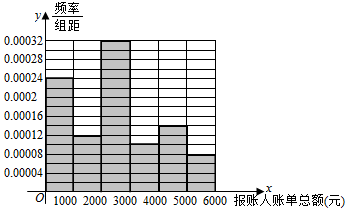
分析 (Ⅰ)由已知先作出频率分布表为,由此能作出频率分布直方图.
(Ⅱ)将频率视为概率从参与节目的报账人中随机抽取3位(看作有放回的抽样),由频率分布直方图得账单总额在[3000,4000)内的报账人数X~B(3,0.1),由此能求出X的分布列、数学期望、与方差.
解答 解:(Ⅰ)由已知得频率分布表为:
| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
| 频率 | 0.24 | 0.12 | 0.32 | 0.10 | 0.14 | 0.08 |
| X | 0 | 1 | 2 | 3 |
| P | 0.729 | 0.243 | 0.027 | 0.0001 |
点评 本题考查频率分布直方图的作法,考查离散型随机变量的分布列、数学期望、方差的作法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
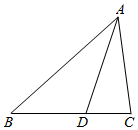 如图,在△ABC中,记$\overrightarrow{BA}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b$,∠B=$\frac{π}{3}$,AB=8,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.
如图,在△ABC中,记$\overrightarrow{BA}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b$,∠B=$\frac{π}{3}$,AB=8,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
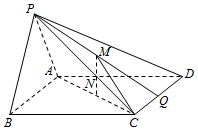 如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com