
| ����x��Ԫ�� | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| ����y������ | 90 | 84 | 83 | 80 | 75 | 68 |
���� ���������⣬�ó�X�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д��X�ķֲ�������ѧ����EX��
������$\overline{x}$��$\overline{y}$�����$\stackrel{��}{b}$��$\stackrel{��}{a}$��д��y����x�����Իع鷽�̣��ó�������L��x���Ľ���ʽ�����ö��κ������������L��x�������ֵ���Ӧx��ֵ��
��� �⣺����X�Ŀ���ȡֵΪ0��1��2������90��x+y��100����3�飬
����P��X=0��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
P��X=1��=$\frac{{C}_{3}^{1}{•C}_{3}^{1}}{{C}_{6}^{2}}$=$\frac{3}{5}$��
P��X=2��=$\frac{{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{1}{5}$��
X�ķֲ���Ϊ
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
���� ���⿼������ɢ����������ķֲ����������ļ������⣬Ҳ���������Իع鷽�̵����Լ����κ�������ֵ���⣬���ۺ�����Ŀ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
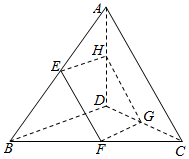 ��ͼ���ڿռ��ı���ABCD�У�E��F��G��H�ֱ���AB��BC��DA���е㣬��AC=BC����֤���ı���EFGH�����Σ�
��ͼ���ڿռ��ı���ABCD�У�E��F��G��H�ֱ���AB��BC��DA���е㣬��AC=BC����֤���ı���EFGH�����Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+3i | B�� | -1-3i | C�� | -1+3i | D�� | 1-3i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [0��2] | B�� | ��0��2] | C�� | ��1��2] | D�� | [1��2] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ���Ҹ��˵�����һ������й��¡������㡢������Ϸ���ֳ������ȶ���Ԫ�ص����մ��ͻ�����Ϸ���Ŀ������ͨ�˽��������˵�����Ĺ��£���������˶�����Ϊ�䶨�ƵĴ�����Ϸ����Ӯ���˵���������ʽ��������������֮������飬չ���˵�����������е�����Ҹ�̬֮��ij���������ȡ100�������Ŀ�ı����˵��˵��ܶ���Ϊ�������з����о����ɴ˵õ�����Ƶ���ֲ�����
���Ҹ��˵�����һ������й��¡������㡢������Ϸ���ֳ������ȶ���Ԫ�ص����մ��ͻ�����Ϸ���Ŀ������ͨ�˽��������˵�����Ĺ��£���������˶�����Ϊ�䶨�ƵĴ�����Ϸ����Ӯ���˵���������ʽ��������������֮������飬չ���˵�����������е�����Ҹ�̬֮��ij���������ȡ100�������Ŀ�ı����˵��˵��ܶ���Ϊ�������з����о����ɴ˵õ�����Ƶ���ֲ�����| �����˵��˵��ܶԪ�� | [0��1000�� | [1000��2000�� | [2000��3000�� | [3000��4000�� | [4000��5000�� | [5000��6000�� |
| Ƶ�� | 24 | 12 | 32 | 10 | 14 | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
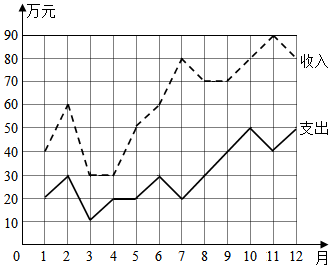
| A�� | �������ֵ���������ֵ�ı���3��1 | |
| B�� | ������ߵ��·���7�� | |
| C�� | 1��2�·ݵ�����ı仯����4��5�·ݵ�����ı仯����ͬ | |
| D�� | ǰ6���µ�ƽ������Ϊ40��Ԫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com