
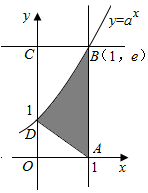
分析 求出AD的方程,利用积分求出阴影部分的面积,结合几何概型的概率公式进行计算即可.
解答 解:AD对应的方程x+y=1,即y=-x+1,
∵点(1,e)在y=ax,∴a=e,
即函数为y=ex,
则由积分的几何意义得阴影部分的面积S=∫${\;}_{0}^{1}$(ex-1+x)dx=(ex-x+$\frac{1}{2}$x2)|${\;}_{0}^{1}$=e-1+$\frac{1}{2}$-1=e-$\frac{3}{2}$,
长方形OABC的面积S=1×e=e,
则点P落在阴影部分内的概率P=$\frac{e-\frac{3}{2}}{e}$=$\frac{2e-3}{2e}$,
故答案为:$\frac{2e-3}{2e}$
点评 本题主要考查几何概型的概率的计算,根据条件求出曲线的解析式,利用积分求出阴影部分的面积是解决本题的关键.


科目:高中数学 来源: 题型:解答题
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
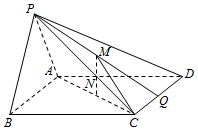 如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
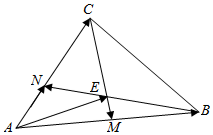 如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.
如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com