
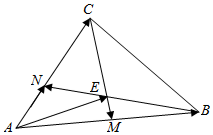
 如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.
如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$. 分析 设$\overrightarrow{NE}$=x$\overrightarrow{NB}$,$\overrightarrow{ME}$=y$\overrightarrow{MC}$,从而分别表示出$\overrightarrow{AE}$=$\overrightarrow{AN}$+$\overrightarrow{NE}$=$\frac{1}{3}$$\overrightarrow{b}$+x(-$\frac{1}{3}$$\overrightarrow{b}$+$\overrightarrow{a}$)=x$\overrightarrow{a}$+$\frac{1}{3}$(1-x)$\overrightarrow{b}$,$\overrightarrow{AE}$=$\overrightarrow{AM}$+$\overrightarrow{ME}$=$\frac{1}{2}$$\overrightarrow{a}$+y(-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{1}{2}$(1-y)$\overrightarrow{a}$+y$\overrightarrow{b}$,从而可得x=$\frac{1}{2}$(1-y)且y=$\frac{1}{3}$(1-x),从而解得.
解答 解:设$\overrightarrow{NE}$=x$\overrightarrow{NB}$,$\overrightarrow{ME}$=y$\overrightarrow{MC}$,
$\overrightarrow{NB}$=$\overrightarrow{NA}$+$\overrightarrow{AB}$=-$\frac{1}{3}$$\overrightarrow{b}$+$\overrightarrow{a}$,
$\overrightarrow{MC}$=$\overrightarrow{MA}$+$\overrightarrow{AC}$=-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$;
∴$\overrightarrow{AE}$=$\overrightarrow{AN}$+$\overrightarrow{NE}$=$\frac{1}{3}$$\overrightarrow{b}$+x(-$\frac{1}{3}$$\overrightarrow{b}$+$\overrightarrow{a}$)=x$\overrightarrow{a}$+$\frac{1}{3}$(1-x)$\overrightarrow{b}$,
$\overrightarrow{AE}$=$\overrightarrow{AM}$+$\overrightarrow{ME}$=$\frac{1}{2}$$\overrightarrow{a}$+y(-$\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$)=$\frac{1}{2}$(1-y)$\overrightarrow{a}$+y$\overrightarrow{b}$,
∴x=$\frac{1}{2}$(1-y)且y=$\frac{1}{3}$(1-x),
解得,x=$\frac{2}{5}$,y=$\frac{1}{5}$;
故$\overrightarrow{AE}$=$\frac{2}{5}$$\overrightarrow{a}$+$\frac{1}{5}$$\overrightarrow{b}$.
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用,属于基础题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:选择题
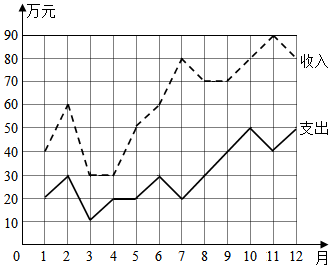
| A. | 收入最高值与收入最低值的比是3:1 | |
| B. | 结余最高的月份是7月 | |
| C. | 1至2月份的收入的变化率与4至5月份的收入的变化率相同 | |
| D. | 前6个月的平均收入为40万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{20}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com