
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 构造函数g(x)=x2-2alnx-2ax,将方程有唯一解,转化为g(x)=0有唯一解,即可求得a的值.
解答 解:由选项知a>0,
设g(x)=x2-2alnx-2ax,(x>0),
若方程x2-2alnx-2ax=0有唯一解,
即g(x)=0有唯一解,
则g′(x)=2x-$\frac{2a}{x}$-2a=$\frac{2({x}^{2}-ax-a)}{x}$,
令g′(x)=0,可得x2-ax-a=0,
∵a>0,x>0,∴x1=$\frac{a+\sqrt{{a}^{2}+4a}}{2}$(另一根舍去),
当x∈(0,x1)时,g′(x)<0,g(x)在(0,x1)上是单调递减函数;
当x∈(x1,+∞)时,g′(x)>0,g(x)在(x1,+∞)上是单调递增函数,
∴当x=x1时,g′(x1)=0,g(x)min=g(x1),
∵g(x)=0有唯一解,
∴g(x1)=0,
∴$\left\{\begin{array}{l}{g({x}_{1})=0}\\{g′({x}_{1})=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{{x}_{1}}^{2}-2aln{x}_{1}-2a{x}_{1}=0}\\{{{x}_{1}}^{2}-a{x}_{1}-a=0}\end{array}\right.$,
∴2alnx1+ax1-a=0
∵a>0,
∴2lnx1+x1-1=0,
设函数h(x)=2lnx+x-1,
∵x>0时,h(x)是增函数,
∴h(x)=0至多有一解,
∵h(1)=0,
∴方程2lnx1+x1-1=0的解为x1=1,
即x1=$\frac{a+\sqrt{{a}^{2}+4a}}{2}$=1,
∴$a=\frac{1}{2}$,
∴当a>0,方程f(x)=2ax有唯一解时a的值为$\frac{1}{2}$.
故选:B.
点评 本题主要考查函数与方程的应用,构造函数,求函数的导数,利用函数极值和导数之间的关系,进行求解是解决本题的关键.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中数学 来源: 题型:解答题
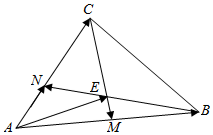 如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.
如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 37种 | B. | 1848种 | C. | 3种 | D. | 6种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com