
分析 (I)设P(x,y),则|PA|2=(x-3)2+y2=(x-3)2+2x=(x-2)2+5,即可求出当|PA|最小时,点P的坐标;
(II)由圆的方程为求得圆心C(3,0)、半径r为:1,若四边形面积最小,则圆心与点P的距离最小,利用距离公式,结合配方法,即可得出结论..
解答 解:(I)设P(x,y),则|PA|2=(x-3)2+y2=(x-3)2+2x=(x-2)2+5,
∴x=2时,|PA|最小,此时y=±2,
∴点P的坐标为(2,±2);
(II)圆C:(x-3)2+y2=1圆心C(3,0)、半径r为:1
根据题意,若四边形面积最小,则圆心与点P的距离最小.
由(I),|PA|最小为$\sqrt{5}$,∴四边形PMAN的面积的最小值为2×$\frac{1}{2}×1×\sqrt{5}$=$\sqrt{5}$
故答案为:(2,2)或(2,-2);$\sqrt{5}$.
点评 本题主要考查直线与圆的位置关系,主要涉及了构造四边形及其面积的求法,同时还考查了转化思想.此题属中档题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 若β=α+k•360°(k∈Z),则α与β终边相同 | B. | 第二象限角一定是钝角 | ||
| C. | 终边在y轴正半轴上的角是直角 | D. | 第四象限角一定是负角 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
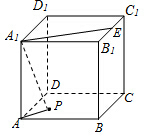 如图,棱长为2的正方形ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P在底面ABCD内,且PA1=A1E,则点P运动形成图形的长度是( )
如图,棱长为2的正方形ABCD-A1B1C1D1中,E是棱B1C1的中点,动点P在底面ABCD内,且PA1=A1E,则点P运动形成图形的长度是( )| A. | 1 | B. | $\frac{π}{2}$ | C. | $\sqrt{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{e}$) | B. | ($\frac{1}{e}$,1] | C. | (1,e) | D. | ($\frac{1}{e}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com