
【题目】设函数![]()
(1)当![]() 时,求函数
时,求函数![]() 的极值.
的极值.
(2)若函数![]() 在区间
在区间![]() 上有唯一的零点,求实数
上有唯一的零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)极小值为![]() ,无极大值;(2)
,无极大值;(2)![]()
【解析】
(1)由a=1,得函数f(x)的解析式,求出其导函数以及导数为0的根,通过比较两根的大小找到函数的单调区间,进而求出f(x)的极小值;(2)求导后按a![]() 进行分类讨论,求出a的范围.
进行分类讨论,求出a的范围.
(1) ![]() 时,
时,![]() 函数的定义域为
函数的定义域为![]()
![]() 令
令![]() 解得
解得![]() 或
或![]() (舍)
(舍)
![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
列表如下
|
| 1 |
|
| - | 0 | + |
| 单调递减 | 极小值 | 单调递增 |
所以![]() 时,函数的极小值为
时,函数的极小值为![]() ,函数无极大值.
,函数无极大值.
(2)![]() ,其中
,其中![]()
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 单调递增,又因为
单调递增,又因为![]()
所以函数![]() 在区间
在区间![]() 上有唯一的零点,符合题意。
上有唯一的零点,符合题意。
当![]() 时,
时,![]() 恒成立,
恒成立,![]() 单调递减,又因为
单调递减,又因为![]()
所以函数![]() 在区间
在区间![]() 上有唯一的零点,符合题意。
上有唯一的零点,符合题意。
当![]() 时,
时,
![]() 时,
时,![]() ,
,![]() 单调递减,又因为
单调递减,又因为![]()
所以函数![]() 在区间
在区间![]() 上有唯一的零点;
上有唯一的零点;
![]() 时,
时,![]() ,
,![]() 单调递增,又因为
单调递增,又因为![]()
所以当![]() 时符合题意,即
时符合题意,即![]()
所以![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有唯一的零点;
上有唯一的零点;
所以![]() 的取值范围是
的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
|
|
| |||
| 0 |
|
|
|
|
| 0 | 3 | 0 | 0 |
(1)请将上表数据补充完整,并写出函数![]() 的解析式(直接写出结果即可);
的解析式(直接写出结果即可);
(2)根据表格中的数据作出![]() 在一个周期内的图像;
在一个周期内的图像;
(3)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方体![]() ,
,![]() 为棱
为棱![]() 的中点,
的中点,![]() 为棱
为棱![]() 的动点,设直线
的动点,设直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,直线
的交线,直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,下列结论中错误的是( )
的交线,下列结论中错误的是( )

A.![]() 平面
平面![]() B.平面
B.平面![]() 与平面
与平面![]() 不垂直
不垂直
C.平面![]() 与平面
与平面![]() 可能平行D.直线
可能平行D.直线![]() 与直线
与直线![]() 可能不平行
可能不平行
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在海岸![]() 处,发现北偏东
处,发现北偏东![]() 方向,距离A为
方向,距离A为![]() 海里的B处有一艘走私船,在A处北偏西
海里的B处有一艘走私船,在A处北偏西![]() 方向距离
方向距离![]() 为
为![]() 海里的
海里的![]() 处有我方一艘辑私艇奉命以
处有我方一艘辑私艇奉命以![]() 海里/小时的速度追截走私船,此时走私船正以
海里/小时的速度追截走私船,此时走私船正以![]() 海里/小时的速度从
海里/小时的速度从![]() 处向北偏东
处向北偏东![]() 方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?
方向逃窜,问辑私艇沿什么方向,才能最快追上走私船?需要多长时间?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,一般情况下PM2.5的浓度越大,大气环境质量越差.右边的茎叶图表示的是成都市区甲乙两个监测站某10日内每天的PM2.5浓度读数(单位:![]() ),则下列说法正确的是( )
),则下列说法正确的是( )

A.这10日内甲、乙监测站读数的极差相等
B.这10日内甲、乙监测站读数的中位数中,乙的较大
C.这10日内乙监测站读数的众数与中位数相等
D.这10日内甲、乙监测站读数的平均数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种设备随着使用年限的增加,每年的维护费相应增加.现对一批该设备进行调查,得到这批设备自购入使用之日起,前5年平均每台设备每年的维护费用大致如表:
年份 |
|
|
|
|
|
维护费 |
|
|
|
|
|
已知![]() .
.
(I)求表格中![]() 的值;
的值;
(II)从这![]() 年中随机抽取两年,求平均每台设备每年的维护费用至少有
年中随机抽取两年,求平均每台设备每年的维护费用至少有![]() 年多于
年多于![]() 万元的概率;
万元的概率;
(Ⅲ)求![]() 关于
关于![]() 的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过
的线性回归方程;并据此预测第几年开始平均每台设备每年的维护费用超过![]() 万元.
万元.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
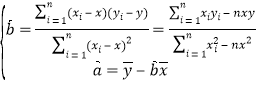
查看答案和解析>>
科目:高中数学 来源: 题型:
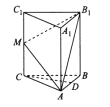
【题目】如图,在三棱柱![]() 中,侧棱
中,侧棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是棱
是棱![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上运动.
上运动.
(1)当![]() 是棱
是棱![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)当直线![]() 与平面
与平面![]() 所成的角的正切值为
所成的角的正切值为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com