
分析 求出M,N的坐标和直线l的方程,设P(x,x-1),得出$\overrightarrow{PM}•\overrightarrow{PN}$关于x的函数,利用二次函数的性质求出最小值.
解答 解:抛物线的焦点F(0,1),∴直线MN的方程为:y=x+1.
联立方程组$\left\{\begin{array}{l}{{x}^{2}=4y}\\{y=x+1}\end{array}\right.$得M(2+2$\sqrt{2}$,3+2$\sqrt{2}$),N(2-2$\sqrt{2}$,3-2$\sqrt{2}$).
设直线l的方程为y=x+b,代入x2=4y得x2-4x-4b=0,
∵直线l是抛物线C的切线,∴方程只有一解.
∴△=16+16b=0,解得b=-1.即l方程为:y=x-1.
设P(x,x-1),$\overrightarrow{PM}$=(2+2$\sqrt{2}$-x,4+2$\sqrt{2}$-x),$\overrightarrow{PN}$=(2-2$\sqrt{2}$-x,4-2$\sqrt{2}$-x).
则$\overrightarrow{PM}•\overrightarrow{PN}$=[(2-x)+2$\sqrt{2}$][(2-x)-2$\sqrt{2}$]+[(4-x)+2$\sqrt{2}$][(4-x)-2$\sqrt{2}$]=2x2-12x+4=2(x-3)2-14.
∴当x=3时,$\overrightarrow{PM}•\overrightarrow{PN}$取得最小值-14.
故答案为:-14.
点评 本题考查了抛物线的性质,直线与圆锥曲线的关系,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
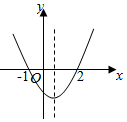 函数f(x)=$\frac{1}{3}$x3+ax2+bx+c(a,b,c∈R)的导函数的图象如图所示:
函数f(x)=$\frac{1}{3}$x3+ax2+bx+c(a,b,c∈R)的导函数的图象如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)与g(x)的最大值不同 | |
| B. | 函数f(x)与g(x)在$(\frac{3π}{4},\;\;\frac{5π}{4})$上都为增函数 | |
| C. | 函数f(x)与g(x)的图象的对称轴相同 | |
| D. | 将函数f(x)的图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,再通过平移能得到g(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
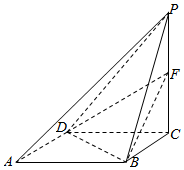 在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PC的中点.
在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PC⊥平面ABCD,且AB=2,PC=$\sqrt{6}$,F是PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com