
分析 将f(x)两边取自然对数,根据对数的运算性质,将其化简为lnf(x)=ln(C${\;}_{10}^{1}$x+1)+ln(C${\;}_{10}^{2}$x+1)+…+ln(C${\;}_{10}^{7}$x+1)+ln(C${\;}_{10}^{8}$x+1),两边对x求导,
化简整理求得f′(x)的解析式,将x=0,代入求得f′(0)=(C${\;}_{10}^{1}$+C${\;}_{10}^{2}$+…+C${\;}_{10}^{7}$+C${\;}_{10}^{8}$),根据二项式定理求得f′(0)的值.
解答 解:两边取自然对数得:lnf(x)=ln(C${\;}_{10}^{1}$x+1)+ln(C${\;}_{10}^{2}$x+1)+…+ln(C${\;}_{10}^{7}$x+1)+ln(C${\;}_{10}^{8}$x+1),
两边对x取导数得$\frac{f′(x)}{f(x)}$=$\frac{{C}_{10}^{1}}{{C}_{10}^{1}x+1}$+$\frac{{C}_{10}^{2}}{{C}_{10}^{2}x+1}$+…+$\frac{{C}_{10}^{7}}{{C}_{10}^{7}x+1}$+$\frac{{C}_{10}^{8}}{{C}_{10}^{8}x+1}$,
故f′(x)=($\frac{{C}_{10}^{1}}{{C}_{10}^{1}x+1}$+$\frac{{C}_{10}^{2}}{{C}_{10}^{2}x+1}$+…+$\frac{{C}_{10}^{7}}{{C}_{10}^{7}x+1}$+$\frac{{C}_{10}^{8}}{{C}_{10}^{8}x+1}$)×f(x)
∴f′(0)=(C${\;}_{10}^{1}$+C${\;}_{10}^{2}$+…+C${\;}_{10}^{7}$+C${\;}_{10}^{8}$)×f(0),
f′(0)=(C${\;}_{10}^{1}$+C${\;}_{10}^{2}$+…+C${\;}_{10}^{7}$+C${\;}_{10}^{8}$),f(0)=1,
故f′(0)=C${\;}_{10}^{1}$+C${\;}_{10}^{2}$+…+C${\;}_{10}^{7}$+C${\;}_{10}^{8}$=210-${C}_{10}^{0}$-${C}_{10}^{9}$-${C}_{10}^{10}$=1012.
故答案为:1012.
点评 本题考查求函数的导数及二项式定理,技巧性较强,要求熟练掌握求函数导数的方法,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,将两个全等的有一锐角为30°的直角三角形ABC和直角三角形ADC 拼在一起组成平面四边形ABCD,若$\overrightarrow{CA}$=x$\overrightarrow{CB}$+y$\overrightarrow{CD}$,则x+y=( )
如图,将两个全等的有一锐角为30°的直角三角形ABC和直角三角形ADC 拼在一起组成平面四边形ABCD,若$\overrightarrow{CA}$=x$\overrightarrow{CB}$+y$\overrightarrow{CD}$,则x+y=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 102 | 126 | 131 | 118 | 127 |
| 乙 | 96 | 117 | 120 | 119 | 135 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
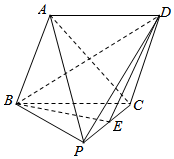 如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.证明:
如图,在四棱锥P-ABCD中,底面ABCD是菱形,侧面PBC是直角三角形,∠PCB=90°,点E是PC的中点,且平面PBC⊥平面ABCD.证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com